| |
СЕРГИЕНКО П.Я. (2021)
РУССКИЙ ПРОЕКТ МАТЕМАТИКИ ГАРМОНИИ.
PDF: https://peacefromharmony.org/docs/Sergienko-Russkiy-proekt-matematiki-garmonii-poznaniya-vsego-sushego-2021.pdf
------------------------
Сергиенко П.Я. Диалектико-триалектическое развитие теории гармонии социальных фракталов тетрасоциологии. 10 июля 2023. «Академия Тринитаризма»: www.trinitas.ru/rus/doc/0016/001h/00165365.htm Писать данную статью меня позвало событие, вокруг которого развернулась обширная международная дискуссия. В июне 2023 года у Льва Семашко, который находился в Дели, индийский журнал WGF взял интервью на английском языке. Ниже его содержание на русском: https://peacefromharmony.org/?cat=ru_c&key=1041
Петр Сергиенко. Персональная страница: https://peacefromharmony.org/?cat=ru_c&key=373 --------------------------------------------
Сергиенко Петр Якубович

142210, г.Серпухов, Московская обл., ул.Октябрьская, 19-Б, кв.30
Тел. дом. (4967) 35-39-48
E-mail: ssp2000@rambler.ru
--------------------------------------------------------------
См. также его другие страницы: https://peacefromharmony.org/?cat=ru_c&key=370 https://peacefromharmony.org/?cat=ru_c&key=373 https://peacefromharmony.org/?cat=ru_c&key=874 https://peacefromharmony.org/?cat=ru_c&key=1018
----------------------------------------------------------------
Здравствуйте, уважаемый Лев Михайлович! Для восстановления нашего взаимопонимания и дальнейшего сотрудничества, советую Вам прочесть мою статью-ответ на вашу постановку задачи математикам: http://www.trinitas.ru/rus/doc/0232/009a/02321107.htm На стр.3 я написал, что для решения поставленной задачи необходимо: «Сложить из 4 фрактальных и равновеликих треугольников фигуру квадрата (прямоугольника) равновеликую данному кругу (сфере).» Данную задачу я смог решить только в 2013 году. Познакомьтесь с ее решением: http://www.trinitas.ru/rus/doc/0016/001d/00162127.htm и почитайте заглавия моих статей на моей персональной странице: http://www.trinitas.ru/rus/doc/avtr/00/0019-00.htm о том какие задачи я еще решал и решил. Фактически все годы я решал сформулированную Вами:
4. Математическая теория фракталов социальной гармонии «золотой тетрасоциологии»
https://peacefromharmony.org/?cat=ru_c&key=370 (2008) «Эта теория является частным случаем предыдущей теории, на которую накладываются ограничения (требования) гармонических «Золотых» пропорций между всеми числами каждой сферной матрицы в их теоретически бесконечном ряду. Фракталы социальной гармонии задаются (определяются) аксиомой сферных гармонических пропорций: для каждого установленного числового значения любого элемента любой сферной матрицы существует гармоническая («золотая») пропорция числовых значений всех других элементов любой сферной матрицы. Или: изменение числового значения любого элемента любой сферной матрицы ведет к изменению всей гармонической пропорции этой матрицы.» Посредством триалектической науки (Триалектика - наука о гармоничном развитии природы общества и мышления) как высшей ступени развития диалектики. Петр Сергиенко. 22-01-23 Математика гармонии глобальной статистики для ее искусственного интеллекта Дорогой Петр Якубович! Во-первых, ГГСГ искренне поздравляет Вас с гениальным и гармоничным, в духе Платона и Пифагора, решением противоречия триа- и тетра-лектики через их синтез /интеграцию в синергии четырех треугольников в квадратах сферных фракталов (ЛИОВ, ПРОП, СИОТ-сферы, СИОТ-сфероны) тетрасоциологии/сфероники, выражающие клеточку научного обществознания и социетальный геном общества на всех уровнях от индивида и семьи до человечества во всем его генезисе. В них треугольники элементов получают недостижимую для них целостность тетрад и выражаются в четырехмерной сферной глобальной статистике, открывающей новую, тетрарную математику гармонии, которую Вы развиваете более 15 лет в ГГСГ (ГСГ) и достигли высшего результаты. Как Платон строил сферы из пирамидок, так теперь Вы строите их, сфер четырехмерность из треугольников, подтверждая истину Пифагора: «Четверица – неиссякаемой жизни источник, царь и Бог всего», воплощённую с сферонике за почти полвека. У меня нет слов, чтобы выразить восхищение Ваших фундаментальным математическим открытием и вкладом в интегральную тетралектику на базе Вашей триалектики в их синергии, а не в противопоставлении, долгое бодание между нами по их поводу, слава Богу, завершилось, как и положено, их гармонией. Ваше письмо на два дня погрузило меня в указанные Вами и мои источники ниже по этой истории, и я не устаю восхищаться Вашей математической гениальностью и великим упорством, твердостьюв ее достижении через 165 трудов только в АТ за 20 лет, не считая почти подобного числа на нашем сайте!! Каковы практические следствия этого? Во-вторых, первое, что в силах ГГСГ, безусловно и в полной мере признать Ваше открытие новой гармоничной математики в приложении к фундаментальной социологии сфероники заслуженным Высшим Почетным Титулом ГГСГ «ГАНДИАНСКИЙ ТВОРЕЦ МИРОВОЙ ГАРМОНИИ» (https://peacefromharmony.org/?cat=ru_c&key=543), что мы сделаем на 18 годовщину ГГСГ 15 февраля с.г. Мы искренне поздравляем Вас и с Вашим гениальным открытием, и с Вашим мировым миротворческим титулом, которому служит Ваше математическое открытие «золотой тетрасоциологии/сфероники». В-третьих, когда мы получим грант на наш стартап «Искусственный Интеллект Глобальной Статистики» (ИИГС) в 4 млн. р., то минимум четверть мы выделим на Вашу работу, под Вашим научным руководством примерно по следующей сопрягаемой теме: «Триалектическая геометрия четырехмерных фракталов сферных статистических матриц сквозной ГлобСтат и его ИИ». Также как вы гениально разглядели треугольники в моих тетрарных сферных моделях на обложке моего учебника «Социология» 1999 г., также гениально вы распознаете цифровые треугольники в статистических матрицах ГлобСтат сфероники, размерностью 4х4n, составляющие ядро/клеточку ИИГС. Эти открытия в синергии сделают Россию мировым технологическим и интеллектуальным лидером нашего века через НАШУ, Вашу и мою, ГГСГ, сквозную цифровую технологию гармоничной «золотой сфероники». Поэтому ищите молодых математиков и программистов для участия в нашем стартапе, копию всех документов которого я Вам вышлю в течение двух недель, когда мы должны будем их закончить. А пока давайте контактировать по этим вопросам по скайпу (мой: leo.semahko). Когда-то давно мы общались с Вами по нему, но скайп я обновил, поэтому звоните. В-четвертых, нас также связывает глубокое общее убеждение нашей долгой жизни, которое Вы блестяще сформулировали так: «Чем глубже я осмысливал начала материалистической диалектики и диалектического материализма (небольшая разница), тем больше убеждался в том, что они стали мировоззренческим тормозом развития науки и общества». https://peacefromharmony.org/?cat=ru_c&key=373. Блестяще!!! Я ограничусь этим, чтобы не трогать мертвого и не уходить от главного, - от создания той фундаментальной, истинно научной и математически доказываемой альтернативы ложного мировоззрения, которое системно обрекло Россию в целом, при всех ее известных, некоторых отраслевых достижениях, на вековое топтание в хвосте запада и его технологий до сих пор. Ваше замечательное письмо и мой отклик опубликованы на 2 Ваших страницах ниже и здесь: https://peacefromharmony.org/?cat=ru_c&key=1007. Лев Семашко, Петр Сергиенко и др. 2008. Математика гармонии и глобальная гармоничная социальная революция начала 21 века: https://peacefromharmony.org/?cat=ru_c&key=362 (1 стр) Лев Семашко, Петр Сергиенко. 2008. Фракталы социальной гармонии и индекс гармонии в «золотой тетрасоциологии»: https://peacefromharmony.org/?cat=ru_c&key=370 (5 стр) Петр Сергиенко. 2009. О началах гармоничной формализации фрактальных матриц тетрасоциологии: https://peacefromharmony.org/?cat=ru_c&key=373 (25 стр) Пётр Сергиенко (2021) Русский проект математики гармонии: https://peacefromharmony.org/?cat=ru_c&key=874 (1 стр) С глубоким уважением, Лев Семашко 24-01-23 ---------------------------------
Сергиенко Петр Якубович
Биография
В моей земной биографии, как в биографии любого человека, имеются свои, особые сюжеты. Родился я 27.6.1938 в год «Тигра» под созвездием Рака. Закончив среднюю школу, осуществил свою мечту - стать авиатором; сдал экзамены в Иркутское военное авиа-техническое училище. Но работать в авиации мне не довелось. Выпускников 1960 года Генштаб направил переучиваться и служить в Ракетные войска стратегического назначения (РВ СН). До 1985 года мой творческий и не творческий труд воинской службы офицера был добросовестно отдан совершенствованию и поддержанию боеготовности РВ СН. Началась служба с должности техника-заправщика, а закончилась преподавателем философии в Серпуховском военном высшем командно-инженерном училище РВ СН.
Мне довелось снаряжать ядерные боеголовки электродетонаторами и пристыковывать их к ракетам-носителям, находиться на боевом дежурстве на земле и под землей, проходить службу на инженерно-технических должностях и должностях политработника. География моей службы обширна; Забайкалье, Украина, Литва, Белоруссия, Казахстан (космодром Байконур).
После увольнения в запас, я стал работать преподавателем философии Всесоюзного заочного института легкой и текстильной промышленности (Московский филиал). Началась эпоха горбачевской «перестройки» и я смог делиться идеями триалектики на занятиях со студентами. Став членом Философского общества СССР (Московская первичная организация), я получил возможность апробации своих идей в среде философов. Чем глубже я осмысливал начала материалистической диалектики и диалектического материализма (небольшая разница), тем больше убеждался в том, что они стали мировоззренческим тормозом развития науки и общества.
Наступило время возрождения древнейших тринитарных идей на более высоком техническом уровне развития цивилизации. Интересно то, что одновременно сходные идеи пришли в головы многих людей, не знающих ничего друг о друге, живущих в разных регионах и не имеющих о том никакой иной информации кроме собственных интуитивных откровений. Наступило время публикации открывшихся идей нового мировоззрения и овладения их массами (в первую очередь управляющими общественным развитием).
Дальнейшая моя биография - в моих научных работах. ---------------------------------------------------
Григорьян Э.Р. Через бездну лжи к мировой гармонии. 2022: http://www.trinitas.ru/rus/doc/0016/001h/00165067.htm (О математическом открытии Петра Сергиенко). Можно поздравить культурное человечество с тем, что оно достигло уровня, с которого вновь может быть адекватно продолжена научная традиция платоновской школы. Наш соотечественник, Сергиенко П.Я., доказал теорему, остававшуюся недоказанной 2,5 тысячи лет, и своими работами внес значительный вклад в развертывание античного и еще более древнего наследия. Это свидетельствует, что разрушительные последствия всяких нашествий не могут окончательно затормозить вечный процесс восхождения к идеальному, с высот которого только и возможно разумное строительство человеческого общества. История длится циклами упадка и подъема, значит мы вступили в фазу подъема, которую и надо использовать в полной мере. Выдающийся ученый и оригинальный мыслитель Сергиенко П.Я. проложил своим творчеством фундированную дорогу для всех наук, а особенно для гуманитарно-социальных. Наконец, все науки получают единый методологический фундамент, обеспечивающий научность подхода. Получили точное обоснование возможность и необходимость гармонизации общественных отношений между цивилизациями Планеты и окружающей ее природы. Открываются новые пути более углубленного познания гармонии жизненных начал, от клетки ДНК до Вселенной. Гармония понимается Сергиенко П.Я. как оптимальная согласованность структурированного бытия Целого и его частей во взаимосвязанной системе. Можно ввести во все учебники его формулу как непреложную аксиому: «Все явления в космосе, их причины и следствия, в том числе, и наше математическое творчество по их познанию, есть результат гармоничного взаимодействия звездных пространственных энергий» (3). Отсюда естественно напрашивается необходимость создания единого интеллектуального координационного центра (искусственного Планетарного интеллекта) гармонизирующего отношения между ноосферной деятельностью цивилизации и Природой. Уходят в прошлое процессы демократизации, массовых голосований толп, не смыслящих в особенностях социальной организации. Все социальные процессы можно удостоверять разработанной Сергиенко математизированной теорией социальной гармонии. А прогресс в обществе достигается, прежде всего, прогрессом в мысли, в более дробной разработке этой теории. Как утверждает Сергиенко П.Я., «в согласии с его теорией, по любой произвольно заданной мере числа можно вычислять и геометрически строить фрактальные структуры и системы мира в гармоничных отношениях любого масштаба. Фундаментальными структурами их построения являются вписанный в окружность прямоугольный гармоничный треугольник и гармоничный тетраэдр, образуемый тремя гармоничными треугольниками» (3). А многочисленная рать сегодняшних чиновников, а по простому – лакейская челядь иноземных олигархов, названная в народе «менагерами» займутся излюбленным распилом, но уже досок для изготовления мебели. И вообще, понятие чиновник должно исчезнуть из лексикона управленцев. Его заменит понятие командной работы, где все равны. Попробуем объяснить какие фундаментальные перемены несут в себе результаты исследований Сергиенко П.Я. Из социологического лексикона исчезают, или переходят во внутреннее употребление, понятия мнения, интереса, предпочтения, выгоды, национального интереса и др. Главным становится соответствие космическому процессу как Целому, в которое входит все мыслимое. Важнейшим условием гармонии Целого и его частей является их пропорциональная соразмерность, которая может быть выражена математически посредством пропорций. Исторические истоки знания алгоритма о пропорциональном отношении «Целого» и его «частей» встречаются в археологических архивах уже 5-6 тысяч лет назад. По крайней мере об этом говорил уже Гермес. В его работах содержатся древнейшие представления о гармонии пространственного мироустройства Космоса. С древних времен и до наших дней, гармония понимается, как оптимальная согласованность структурированного бытия Целого и его частей во взаимосвязанной системе. Работы Сергиенко П.Я. вполне согласованы с мнением древних и выступают как их дальнейшее развертывание ( См. 4, 5, 6, 7). Сергиенко П.Я. в течении четверти века, изучал, осмысливал и переосмысливал учения древних мыслителей (в том числе, Парменида, Пифагора, Гераклита, Платона) и Символ Святой Троицы о гармоничном устройстве космического бытия. Кстати, в русло этих дискуссий укладывается и спор между монофизитами и диофизитами - между армянской и византийской церковью. Последняя исповедовала наличие двух природ – божественной и человеческой. Монофизиты же, признают одно лицо, одну ипостась и одну природу. Т.е., ведущее свое начало от Гермеса армянское христианство получило научное обоснование своей правоты в работах Сергиенко П.Я. Переосмысление древних знаний триалектическим методом познания, привело его к принципиально новым математическим знаниям арифметических и геометрических начал иерархии структурной гармонии, а также фрактального мироустройства космоса от электрона до Вселенной. Платоном была сформулирована без доказательств геометрическая теорема, которую потомкам надлежало доказать, чтобы открыть сакральную меру гармоничных отношений действительного мира. Сергиенко обнаружил кодовый ключ к доказательству этой теоремы Платона и открытию им «сакрального» треугольника (метатреугольника) как радикальной меры фрактальной закономерности, проявляющейся в симметричных отношениях ряда сторон равнобедренного прямоугольного треугольника и квадрата (См. 1). Методологическим основанием для разработки алгоритмов пространственной гармонии Сергиенко П.Я. избирает три постулата триалектической логики, отражающие реальность бытия космического пространства: 1. В мире нет ничего кроме движущихся пространств (электромагнитных, плазменных газообразных, жидкообразных, кристаллообразных, световых, цветовых, звуковых, химических, биологических, психических, экономических, политических, финансовых, математических и многих других, оформленных или бесформенных пространств); 2. В мире нет такого целого, которое не являлось бы частью другого, относительно большего целого. (Об этом говорил уже Гермес). 3. Учение Платона об устройстве тела космоса и его гармоничной жизни. Триалектика – наука о всеобщих законах гармоничного разрешения противоречий природы, общества и мышления. Во многом она схожа с методологией Гермеса, за исключением, разве что, математических построений. Особенно важно доказательство со стороны Сергиенко П.Я. положения, что мир устроен по принципу не просто гармонии, а – предустановленной гармонии изначально. Это принцип всеобщих гармоничных (пропорционально равных) отношений между существующими в единстве противоречивыми принципами бытия – изменения и сохранения. В литературе этот принцип прижился как «золотая пропорция». Суть поиска «золотой» (пропорциональной гармонии) между пространствами целого и его частями направлено к тому, чтобы выявить единую пространственную меру для целого и его частей, а также алгоритм построения и вычисления количественных мер и отношений в триаде, при которых указанные отношения будут соответствовать отношениям «золотой пропорции». То есть алгоритм, даже в социально-организационных структурах должен соответствовать следующим формально-логическим условиям: 1. Для пространств всемирной организации Целого и его частей – государств, корпораций, наций, общин, просто дружеских коллективов и социальных групп должна быть единая мера. 2. Отношение пространственной меры большей части к мере меньшей части должно быть численно равно отношению меры Целого к мере его большей части. Например, любая социальная иерархия должна строиться по принципу: как мера организации космоса относится к человечеству вообще, так и любая организованная часть человечества должна относиться к своей малой внутренней части. Или иначе, и более понятно: как бог относится ко мне, так и я к тебе. Здесь совершенно стирается разница между наукой и «правильной» религией. И там и там идет речь о необходимости построения единого правильного образца поведения, которому следовали бы все люди и во всех обстоятельствах. И аналогично, речь должна идти о построении таких социальных организаций, которые мотивировали бы такое поведение. Социальная система включает иерархию уровней своей организации: «индивид - семья - род - народ - общество». Эти уровни образуют ядро всей мировой социальной системы, и они фрактально составляют ментальную и биологическую наследственную основу индивида и общества. Они должны находиться во взаимоотношениях золотого сечения (чисел Фибоначчи), чтобы соответствовать природной гармонии. Но варварское состояние человеческой культуры, которое достигло небывало низкого уровня именно в 20 веке, не смогло развить новую педагогику и этику семейных отношений, соответствующую переходу на новый уровень сознания. Естественным видится, в свете дальнейшего подъема, поставить под общечеловеческий запрет все формы колониальных порабощений, подвергнуть осуждению нацистские режимы и социальные организации, прославляющие «избранные» народы, табуировать все формы идеологий, проповедующих господство одних над другими. Должна будет со временем покинуть Землю и ветхозаветная пропаганда такого рабства, как и вообще пора убраться обратно в пустыни Аравии носителям таких взглядов. Опасна не столько преступность, сколько ее идеологическое оправдание. Павликианское движение, насчитывающее уже тысячи лет, давно сформулировало эти требования (см.6). В мире останутся социальные фрагменты Целого, которые равнозначны или равносильны, независимо от того, какое место они занимают в структурной иерархии. Специфичность каждого из них проявляется посредством единой относительной меры их пропорциональных отношений в границах целостности. Повторим ранее сказанное еще раз: не просто вести себя по принципу «Как ты ко мне, так и я к тебе», а учитывать структурную иерархию Вселенной, которую можно полагать числовым рядом Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, … Сергиенко П.Я. довел до теоретического завершения зачатки «Математики гармонии» – завещанные предыдущими мыслителями алгоритмы, моделирующие гармонию бытия пространственно-временных форм жизни, их количественные отношения, проявляющиеся в эволюции природы, общества и мышления. Он показал гармонию как равенство пропорциональных отношений между различными частями Целого. Например, между музыкальными октавами, между противоположными частями архитектурного здания, между членами семьи, между городом и деревней, между мировой системой и входящими в нее политическими объединениями и т.д. Более четверти века Сергиенко П.Я. искал геометрический и числовой ключ (код), который бы открыл онтологические начала природной простоты «порождающей модели», как структурного начала математического моделирования знаний о гармоничном космосе. Мироустройство космического бытия было закодировано в мистических учениях Пифагора и Платона, унаследовавших знания египетских мудрецов, Гермеса, в числе первых. Таким ключом является построение сакрального треугольника и доказательство теоремы Платона, которую Платон формулирует без доказательства устами мифического Тимея, подводя итог описания жизни космоса. И которую, впервые за 2.5 тысяч лет, доказывает Сергиенко П.Я. В согласии с принципом предустановленной гармонии, все мировые константы математически связаны между собой посредством некой единой меры. Ученые полагают, что большинство известных констант естествознания связаны между собой посредством математической константы π = 3,1415926… Работая в Госстандарте, Сергиенко П.Я. узнал, что экспериментально значение данной константы никогда не проверялось. Предложенный им, и одобренный начальником Госстандарта, довольно простой эксперимент, к сожалению, так и не проводился. Вычисленное Сергиенко П.Я. более точное численное значение пи равно ��с = ��, �������������������������������������������������������������� …, что приближенно на 0,09% отличается от повсеместно применяемого значения π. Это означает, что все использующие стандартное значение пи расчеты неверны. Это касается и всех форм измерений, применяемых в стандартизации продукции. По мнению многих ученых, изменение мировой константы даже на незначительные числовые значения меньшие единицы, ведет к пересмотру всей картины мира. (См.1). В результате вычисления константы ���� впервые стало возможным: 1. Построить прямоугольную систему гармоничных ординат. 2. По любой произвольно заданной мере (числу) построить гармоничный тетраэдр. 3. По любой произвольно заданной мере числа построить правильную 5-гранную пирамиду, у которой все ребра равны. Вычислять гармоничные параметры структурного устройства Платоновых тел – додекаэдра, икосаэдра. А главное, впервые получена возможность, выражаясь техническим языком, абсолютно точно «стыковать» метрику измерений пространства формальной математики с метрикой метапространства. Вычисление констант предустановленной гармонии на основе константы πс позволило автору Сергиенко П.Я. создать математическую модель относительно гармоничных удалений созвездий друг от друга по окружности зодиака и относительного распределения мощности световой энергии созвездий в зодиакальном круге нашей галактики, вдоль которых происходит периодически повторяющееся, примерно каждые 26000 лет, движение нашей Солнечной системы. Перечислим кратко еще ряд достижений Сергиенко П.Я. Впервые геометрический символ Инь-Ян разделен на асимметричные части в отношениях «золотой» пропорции. Представлена математическая модель Инь-Ян в ее пространственной форме и количественных мерах параметров, как системы. Исследование данной системы позволяет получать информацию о гармоничном взаимодействии двух противоположных электромагнитных энергий звездного пространства - света и тьмы (отсутствия света). В результате открытия метрических параметров метатреугольника, их геометрических и численных закономерностей были заложены начала «живой математики» гармонии ноосферного образования и просвещения. Созданы НАЧАЛА геометрии ближайшей к обыкновенной геометрии Евклида. То есть, автором реально решена 4-я проблема Гильберта, в согласии с его формулировкой: «Более общий вопрос, возникший при этом, заключается в следующем: возможно ли ещё с других плодотворных точек зрения построить геометрии, которые с таким же правом могли бы считаться ближайшими к обыкновенной евклидовой геометрии». Автором Сергиенко П.Я. описан подробный оригинальный алгоритм построения «золотых» мер и пропорций пирамиды Хеопса методом и инструментами древнего архитектора Хеси Ра. Самым замечательным в ее построении является простота точного строительства треугольных граней пирамиды, возвышающихся до центральной «точки» вершины более, чем стометровой высоты пирамиды (См. 1.). Завершая наш обзор достижений Сергиенко П.Я., добавим, что некоторые математические закономерности, алгоритмы и численные константы, например, гармоничного деления круга круговыми движениями и прямыми линиями, в учебниках элементарной математики отсутствуют. Основное его открытие повторим еще раз: по любой произвольно заданной мере числа можно вычислять и геометрически строить фрактальные структуры и системы мира в гармоничных отношениях любого масштаба. Фундаментальными структурами их построения являются вписанный в окружность прямоугольный гармоничный треугольник и гармоничный тетраэдр, образуемый тремя гармоничными треугольниками. И в заключение процитируем окончание его статьи: «Сергиенко П.Я. Р.Фейнман о научной проблеме КЭД и ее решение автором» (2). «В феврале 2018 года состоялся юбилейный форум Римского клуба: «Старый Мир обречен. Новый Мир неизбежен!». На этом форуме его сопредседатель Андерс Вийкман сделал заявление: «2020 год – год фактической смерти Старой Системы. Отныне Мир должен принять Новый Путь – ведущий к общей справедливости и гармонии социума, экономики и природы. Иначе – смерть всей цивилизации!». Данное заявление о предшествующей эволюции цивилизации, о гармонии социума, экономики и природы по времени совпадает с эволюцией КЭД на основе метагеометрии гармоничного мироустройства. К сожалению, Мир Старой Системы не принял Новый Путь - ведущий к общей справедливости и гармонии без силового принуждения. К несчастью, началась кровопролитная война, которая проявляется в настоящее время как временная часть эволюционной необходимости гармоничного мироустройства природы, общества и мышления на планете Земля по изначально предустановленным законам Творца. Согласно этим законам, человечество Земли в 21 веке должно подняться на высшую ступень своего развития, на ступень со-Творца, а не только потребителя» (2). Ряд приложений его теории изложены в публикации «Сергиенко П.Я. Новые знания математики гармоничного мироустройства», помещенной на нашем сайте. Литература 1.Сергиенко П.Я., Русский проект математики гармонии познания всего сущего // «Академия Тринитаризма», М., Эл № 77-6567, публ.27027, 12.03.2021 http://www.trinitas.ru/rus/doc/0016/001h/00164650.htm 2.Сергиенко П.Я., Р.Фейнман о научной проблеме КЭД и ее решение автором // «Академия Тринитаризма», М., Эл № 77-6567, публ.27697, 13.03.2022 3.Сергиенко П.Я., Новые знания математики гармоничного мироустройства // «Академия Тринитаризма», М., Эл № 77-6567, публ.27980, 16.07.2022 4.Григорьян Э.Р. АЛГОРИТМ ГЕРМЕСА КАК ДИАЛЕКТИКА ГАРМОНИИ (от 15.01.2020) 5.Григорьян Э.Р. Обновленная роль третьей силы 6.Григорьян Э.Р. ПОЧЕМУ ПАВЛИКИАНЕ ОТВЕРГАЛИ ВЕТХИЙ ЗАВЕТ? 7.Григорьян Э.Р. КАК ПРЕОДОЛЕТЬ БИПОЛЯРНОСТЬ МЫШЛЕНИЯ ----------- Э.Р. Григорьян, Через бездну лжи к мировой гармонии // «Академия Тринитаризма», М., Эл № 77-6567, публ.28002, 29.07.2022 ======================= Э.Р. Григорьян Социальные приложения теории гармоничного развития Новые методы научного мышления проникли широко в естественную науку. Без таких понятий как фрактал, бифуркация, структурный резонанс, когерентность, золотое сечение и гармонизация научная статья смотрится обедненной. Причем, предмет исследования, стремясь достичь Целого, становится все шире, перешагивая все дисциплинарные ограничения и классические разделения наук. Заповеди Гермеса, изложенные в «Изумрудной скрижали», снова, как и в древности, становятся настольным руководством ученого. Учебники и учебные пособия для вузов также переходят на новую научную платформу, реализуя тот искомый подход к образованию, который кажется назревшим, но официально не озвученным. Хотя этот подход проник и в социальные науки, и десятки лет ведутся отдельные исследования, тем не менее общественный дискурс безнадежно отстает от наукоемких понятий и кажется архаизмом 19 века, с помощью которого пытаются объяснить явления века грядущего. Особенно резок разрыв между массовым сознанием, не различающим ядовитые или здоровые коренья знаний, и академическими научными институтами, наглухо закрывшими свои двери от общественных диссонансов. Эту лакуну спешно заполнили комментаторы, партийные и общественные лидеры, политические активисты, нанятые мощными корпорациями, сосредоточенными на жизненно важных собственных интересах. И страна, имеющая передовую науку, завязла стреноженными ногами в болоте навеянных предрассудков. Народ деградирует, поскольку окучивается чуждыми силами, а наука безмолвствует, поскольку не имеет доступа на общественную активность. Там толпятся только «признанные». Но все равно, без науки развитие невозможно, и смело прогнозируем поворот общественного внимания к достижениям социальных наук. В свете этих веяний статья посвящена переходу этих наук на указанную методологию и излагает успешные попытки по иному осмыслить происходящее в мире, который является всего лишь продолжением природы и космоса. Краеугольным камнем для нового осмысления социальной сферы мы полагаем принцип Золотого Сечения, пронизывающий все целое, подчиняющееся закону гармонического деления. Из него вытекает и широко известный в физике принцип минимального действия. В социальных науках он применяется в социальной инженерии, вошел как элемент Теории гармоничного развития в разработанную П.Я.Сергиенко философско-методологическую платформу «Триалектика» (1). Экономия действия, принцип минимального действия прослеживается всюду. Например, как работает вирус? Он просто использует много раз один и тот же участок нуклеиновой кислоты для синтеза большого числа стандартных молекул — строительных белков, объединяющихся в процессе автосборки вирусной частицы. В результате достигается максимальная экономия генетической информации. По законам математики для построения наиболее экономичным способом замкнутой оболочки из одинаковых элементов нужно сложить из них икосаэдр, который наблюдается в структуре формы вирусов. Так «решают» вирусы сложнейшую задачу: найти тело наименьшей поверхности при заданном объеме и притом состоящее из одинаковых и тоже простейших фигур. Все живое борется за увеличение структуры при поглощении солнечного излучения, а не за её уменьшение, как описывает эволюцию второй закон термодинамики. Те же процессы протекают и в социальной сфере, и там социум стремится найти структуры, позволяющие функционировать экономично и оптимально. (См. 2). И особенно, принцип минимальности вытекает из фрактальности построений, достигаемых сакральными треугольниками и другими подобными фигурами. Открытия П.Я.Сергиенко Сакральных треугольников или «Метатреугольника» (2), заложили основы уже не только математической, но и природной теории развития всего живого. Недаром П.Я.Сергиенко называет число 1,618 “Константой гармоничного мироустройства”. Теперь и перед социальной наукой возникает возможность переосмыслить все текущие и исторические события – войны, революции, вторжения, колонизацию, реформы, смену власти и др. с точки зрения этого общеприродного принципа и точных математизированных моделей Гармоничного развития. Тем более, что именно при его посредстве выстраивается долгожданная гармония, к которой причастен и ряд чисел Фибоначчи, материализуемый в форме спиралей филлотаксиса. Именно на основе этого принципа выстраивается и конструкция фрактала – самоподобно развивающейся структуры. Природа старательно ищет и вычерчивает один единственный шаблон, который применяет во всех случаях. Например, резонанс гармонизирует жизнь и работу организма на основе золотой пропорции, поскольку вся биосфера Земли вовлечена в поля различных колебательных процессов, и в процессе эволюции организм человека наилучшим (гармоничным) образом приспособился к этим условиям. Т.е., предельная экономия усилий достигается тем, что всюду можно опираться на один и тот же инструмент, изменяющийся только в масштабном измерении. И этот шаблон становится далее эталоном для построения всех иных форм живого. «Метатреугольник», который нашел П.Я.Сергиенко, можно считать идеальным объектом природы. Причем в единственном варианте. И подобные объекты свидетельствуют о реальных природных шаблонах, которых надо придерживаться при организации социальных форм с приложением при этом наивозможно минимальных усилий. Интересно, что для нахождения таких гармоничных или «сакральных» фигур, достаточно знания только одного параметра – все остальные параметры выстраиваются автоматически. Даже в многомерном пространстве. Пример таких объектов – Золотые платоновы тела. И теперь перед социальными науками стоит задача формирования новой гармонии отношений внутри человечества, на нашей планете и в ближайшем Космосе. Онтологическое единообразие природы требует унификации и научных подходов. Принцип пропорционального развития предстает наиболее экономным способом, которое теперь нужно использовать и социальными науками. Любое другое направление действий по решению социальной задачи будет привлекать больший объем усилий и, вполне возможно, превысит баланс отдачи от ее решения. И как найти этот путь? Конечно, сразу возникает апелляция к множеству разнородных социальных субъектов, находящихся в разных контекстах и обремененных разными социальными задачами. Заметим, что сегодняшний социальный дискурс слишком индивидуализирует различие культур, психологий, этнических и территориальных особенностей различных стран и народов. Опираясь на фрактальное построение культуры, социальной организации, особенностей поведения тех или иных этносов и народов, социальная наука давно уже могла бы представить человечеству некую приблизительную таблицу характеров многих народов, которые не изменяется в течение тысячелетий. Фрактальное построение процесса развития народа уподобляется дереву с ветвящимися видоизменениями, не нарушающими общий принцип его существования. Более того, поскольку допуск к существованию на планете дается санкцией Целого, то народы (части Целого), не совместимые с Целым, не долговечны. Следовательно, все части социального мира уже априори на данный момент совместимы друг с другом. Правда, процесс этот продолжается, поскольку ничего конечного в природе не существует. Вопрос только в сознательном использовании этих пропорций в построении социальных организаций и иерархии их ступеней. Вот здесь и начинаются ловушки в виде, например, государственных и надгосударственных устройств, которыми обязано заняться обновленное социальное мышление. Несколько усиливая этот тезис, скажем, что в мире существует лишь одна общечеловеческая культура. Та, которая совместима с природными и космическими законами. Значит, и во всех социальных процессах Природа пользуется тем же минимумом всеобщих мер, посредством которых выстраивается гармоничное сосуществование бесконечного многообразия ее форм. Поскольку в них входят и социальные формы и международные отношения, то опорой их здорового единства может послужить наука о законах гармоничного разрешения противоречий и противоположностей, находящихся в единстве Целого иерархически устроенной системы. Сформулированная П.Я.Сергиенко (2) наука «Триалектика» даже больше подчеркивает умаляемое обычно единство и взаимосотрудничество этих противоречий, а не только обычный акцент на их борьбе. Он также утверждает, что масштабно структурная иерархия мироустройства космоса проявляется по принципу “Золотого сечения” (см. 2). Т.е., в этом сечении сливаются красота, минимальность усилий и идеальная точность. В принципе сегодня более остры социальные противоречия, нежели природные, и может быть, пора находить их гармоничные решения. Значит вопрос можно сформулировать иначе: почему их не так скоро находят, ведь общеприродные законы гармонии имеют универсальный характер, приложимы ко всем структурам природы и общества на всех уровнях их организации и обязательно должны вскрываться и в социальной сфере. У сторонников плюрализма в общественных науках легко возникает возражение. Они говорят: взгляните теперь на социум и поищите там гармонию. Да, есть великое разнообразие мнений, оценок, точек зрения. Любая вещь в социуме, кажущаяся красивой в данное время и в данном месте, может оказаться некрасивой при других обстоятельствах. Это также относится и к мыслям, словам, поступкам. Да это есть. Но взглянем с другой стороны. Мы можем отыскать гармонию в вещах, и она будет независимой от мнений. Гармония сочетания цветов, гармония очертаний и линий составляет то, что мы зовем красотой; а слово, чувство, мысль или действие, которые творят гармонию, являются производными от объективной красоты пропорций. То, что мы называем прекрасным, является таковым не только лишь в определенное время и в определенных условиях, которые делают это прекрасным. Построенное по правилам гармонии изделие должно быть таковым для всех людей и всех исторических эпох. Но точно такой универсальностью должно обладать и конструирование социальных форм. У науки социологии наконец-то появляется твердое основание ее научной обоснованности. А исторические исследования могут вскрыть причины исчезновения многих народов, вытекающие из принятия «негармоничных» форм социального устройства. В чем неизбежность такой их кончины? В третьей части цикла «У водоразделов мысли» П.А.Флоренский задает этот вопрос и отвечает на него: «Если закон золотого сечения есть закон красоты, то почему ему должны подчиняться не только произведения изящных искусств, но и произведения природы (по обычному воззрению), не зависящие в своем строении от творческой воли человека? Было бы столь же чуждо произведениям искусства не подчиняться этому закону, как и произведениям природы ему подчиняться, если бы золотая пропорция была пропорцией именно эстетической. Но мы знаем, что ей подчинены явления природы, и, следовательно, золотая пропорция эстетической бывает в своем частном или, точнее, вторичном причинении, но не в своем первоистоке» ( 3, с.468). Поэтому применяющиеся иногда двойные стандарты, равно и циничная ложь есть не только недостойный аморализм, но симптомы распадающегося на части социума.
Гармония – по греч. armonia – связанность и соразмерность частей – установка культуры, ориентирующая на осмысление мироздания как в Целом, так и его фрагментов, в том числе человека и социума, с единой и единственной точки зрения, с позиции полагания их глубинной внутренней упорядоченности и единства с Целым. Гармоничное соединение всего малого в большое создает красоту. Гармоничное поведение должно воспроизводить себя самоподобным и самовоспроизводящим образом. Оно должно быть точкой, отступить от которой – значит впасть в дисгармонию. Это означает, что каждый человек должен демонстрировать такое поведение, что уподобление ему не вызовет противоречий ни в ком и ни в чем. Но бесконечное множество контекстов, ситуаций, обстоятельств, в которых взаимодействуют люди, вызывает потребность в таком же множестве образцов, канонов, эталонов, соответствующих этим уникальным обстоятельствам. Обучиться всему этому разнообразию невозможно, но применять один и тот же принцип велено природой и ее принципом минимальных усилий. Если во всех профессиях требуется хорошее знание своего дела, то для всех сфер, имеющих дело с человеком – медицина, образование, торговля, управление и др. –критерием приема работника должно стать выполнение им правил гармоничного общения. Но мы не превозносим гармонию, как могло бы показаться. Мы просто даем точку отсчета для обсуждения качества форм социальной организации. Пока не известен эталон для данных индивидуальных обстоятельств социальной деятельности, нельзя говорить о степени совершенства ее воспроизведения. Идеальная организация пожарной деятельности отличается от идеальных условий обучению игре на скрипке. Более того, гармония имеет и свои отрицательные моменты. Приближение к гармонии может способствовать стагнации, застойному существования, потере мотивации к действию. Может быть поэтому, гармонию склонны искать люди, уставшие от конфликтов. А ведь активные и полные сил и энергии молодые люди скорее ищут поводов для развития, даже путем излишнего напряжения сил, не избегая и конфликтов. Гармония и лад - не всегда способствуют развитию, а то и прямо препятствуют ему. И в ряде обстоятельств, развитие, рост разнообразия могут стать более приоритетными. Дисгармония - нарушение гармонии, отсутствие созвучности; неблагозвучие, несогласованность, нарушение соответствия чего-либо с чем-либо. Дисгармония столь же многомерна, как и гармония. Для разных компонент, составляющих систему, гармония и дисгармония выглядят по-разному: если для одной компоненты наступает гармония, то для другой такое сечение не является гармоничным и наоборот. Например, будет ли смотреться гармоничной игра на скрипке рядом с тушением пожара? Таким образом, возникает проблема согласования частичной гармоничности для компонент, составляющих систему. Приведем пример применения золотого сечения для оценки различных структур общественных социально-экономических систем на предмет наличия или отсутствия у них гармонии. В работе Кирия В. Г. «О золотом сечении и гармонии в амбивалентных системах» (4) показаны соотношения между социальными слоями общества для современной России, Китая и Европы в 2001 г. Для России это 0,05 - класс богатых, 0,20 -средний класс и 0,75 - класс бедных. После сопоставления по определенной формуле этого соотношения с золотой пропорцией, делается вывод, что современная структура России имеет слабую гармонию. Аналогично, расчет для точек дисгармонии показывает, что такая структура России содержит достаточно высокую дисгармонию. Далее проводятся расчеты по структуре Китая 2001 г.: 0,15-0,25 богатый класс, 0,50 -0,60 средний класс и 0,15 - 0,30 нижний слой населения. Сравнивая это разделение с золотым сечением, автор приходит к выводу, что это сильная гармония. Затем [там же] приведены данные о структуре населения для Европы: 0,07 удельный вес высшего класса, 0,62 - среднего и 0,31 - низшего класса. Рассчитав расстояние между точками золотого сечения для различных автор находит, что имеет место достаточно высокая гармония. Интересно было бы сравнить эти показатели у ряда стран. Например, у Турции могла бы преобладать дисгармония, ввиду ее непрерывного выноса вовне внутренней конфликтности, ее переноса на отношения с другими странами. Дисгармоничность – это когда социум не ладит с самим собой. Дисгармоничность – это разорванная, конфликтная атмосфера, терзаемая изнутри внутренними и внешними проблемами. Но, дисгармония проявляется и в отношениях с внешним миром. Бросим взгляд на общую картину нашего социума через ТВ или медиа. Ежедневно мы слышим взаимную критику, слова оскорбления и сообщения о противоправных действиях, продиктованных неприязнью или ненавистью. Они встречают негативный отклик у задеваемой стороны, и это создает еще большую дисгармонию в социуме. Нашими ежедневными гостями по ТВ давно уже стали полиция, суды, прокуратура, адвокаты и законодатели. Дисгармония создает дисгармонию, и она будет множиться, если мы позволяем ей расти. Откуда же изначально берутся великие разногласия, волнения и раздоры, которые мы сейчас видим преобладающими в мире? Похоже, из незнания или пренебрежения тем фактом, что существуют и иные, гармоничные реакции, останавливающие расширение дисгармонии. Да, если человека оскорбляют, в нем возникает естественная тяга ответить еще большим оскорблением. В результате он получает кратковременное удовлетворение, что он отомстил обидчику. Но та энергия, что исходила от обидчика, повлияла на него, и эти две силы, будучи негативной и позитивной, создали еще большую дисгармонию, открылся новый фронт военных действий. А если мы введем в социум правило отвечать не дисгармонией, а найденным для данного контекста гармоничным решением, словом, действием? Стремление к гармонии можно сравнить со скалой в море: в ветер и бурю она твердо стоит; волны яростно набрасываются на нее, но скала выдерживает их натиск, позволяя им биться о себя. Борясь с дисгармонией с помощью полиции, мы увеличиваем ее. Отказываясь от борьбы с ней, нейтрализуя ее собственным поведением, мы отстраняемся от подливания масла в огонь, который в противном случае увеличился бы и повлек за собой больший пожар. Несомненно, что чем мудрее мы становимся, тем с большими трудностями мы сталкиваемся в жизни, потому что любая дисгармония еще дальше отстоит от ожидаемого нами поведения. В этом положении есть свои преимущества, ведь всякий раз, когда мы выдерживаем напор дисгармонии, это помогает ее разрушить и увеличивает наши силы – так что в любом случае мы становимся сильнее, хотя внешне, для далеких от этого понимания людей, оно кажется поражением. Мы вступаем в поле поисков гармоничных решений, и они усиливают нас. Но тот, кто осознает увеличение своей силы, находясь на правильном пути, больше не сочтет себя побежденным. Он не скажет преждевременные слова и не начнет отвечать, не дослушав вопрос. Слово несогласия, пусть и сказанное во время спора, он воспринимает как временный диссонанс, и сам спор стремится превратить в гармонический аккорд. Наши теледебаты, намеренно или нет, очень далеки от этого понимания. Достижение гармонии в жизни достигается тем же путем, что и умение музицировать, хотя требует еще более продолжительного и серьезного изучения, чем развитие музыкального слуха и голоса. Поэтому кардинальный путь развития общества – это умножение гармоничного саморазвития, рост мудрецов, а не количества партий. Еще один пример приложения правил Золотого сечения к социальной сфере изложен в статье Б.С. Златеева «О применении закона золотого сечения к историческому процессу» (5). Автор провел исследования истории Византии, Арабского халифата, Оттоманской империи, средневековой Болгарии, Китая, Японии, Эфиопии, которые показали, что узловые точки золотого вурфа (тройное Золотое сечение), в соответствующем масштабе наложенного на временную ось и ориентированного на ней в направлении уменьшения отрезков, соответствуют важным событиям в истории каждого из исследуемых государств. Т.е., пропорции Золотого сечения образовали временные интервалы важных изменений в истории этих стран. Как указывает автор, если конец исследуемого периода не известен, а также если нельзя определить его начало, золотой вурф лучше всего выстроить по двум важнейшим историческим событиям, данные которых определены точно, и попробовать поместить между ними разное количество узловых точек. Эти две даты называют опорными. Один из полученных таким способом вариантов дает совпадение остальных узловых точек с другими важными историческими событиями, и таким образом, золотой вурф определяется однозначно. В тех случаях, когда государство продолжает существовать, конец периода его существования нельзя определить даже приблизительно и можно построить несколько разных вариантов для части золотого вурфа в зависимости от того, какие узловые точки принять за главные и какие — за второстепенные. Подобные темы могут быть предложены для исследования студентам и аспирантам, результаты которых, наверняка, будут очень полезными и для сферы международных отношений. Возможная таблица характеров народов пополнится стадиями их становления. Дисгармония появляется и от неправильной социальной организации. При ней люди считают нормой то, что в действительности является болезнью ума. Рассмотрим бросающееся в глаза чрезмерное обилие в нашем социуме контролирующих инстанций. Они борются с плохим, вместо того чтобы сеять хорошее. Их задача - осуждать и пресекать нехорошее. Но нехорошее только растет и подавляет ранее здоровый социум. Ведь понятие идеального поведения, идеальной нормы вытравлено из сознания. Ни дети, ни взрослые не знают ее и, следовательно, будут бесконечные споры. А идеальная норма экономит энергию, сокращает путь к синтетическому решению жизненных проблем. Т.е., решение содержит связность и соразмерность со всеми параметрами социума, т.е., оно – гармоническое. Тогда и все вещи вокруг вступают в те же отношения. Если родитель правильно заботится о детях, учитель - справедлив, а управленец – честен, то и дети усваивают это правильное отношение к другим. Следовательно, в любой социальной иерархии, сверху донизу должно работать одно и то же правило: высшее так относится к среднему, как среднее к низшему. Конечно, его можно интерпретировать по-разному, в том числе и в режиме грабежа. Но речь идет о стабильных структурах социума, не приводящих к его исчезновению. К числу контролирующих инстанций относятся и многочисленные организации по правам человека, детей, животных, меньшинств, инвалидов, мигрантов и т.д. Люди получают большие суммы денег и полномочий, борясь против нарушений в этих правах. Если этих нарушений не будет, то они перестанут получать деньги. Поэтому, когда этих нарушений мало, их придумывают, чтобы не лишиться кормушки. Изобретают разного рода фальшивые прецеденты, имитируют бессознательную предвзятость и микроагрессию по отношению к этим слоям и требуют больших сумм для устранения этих прецедентов. Это стандартная логика небольшого ума. Они не хотят стать безработными. Именно поэтому они будут плодить дисгармонию, поощрять ее расширение, выдвигая все более надуманные теории и нести откровенную бессмыслицу, ссылаясь на то, что жизнь – это борьба противоположностей. Но корень проблемы глубже. Он в том, что постоянная ложная опека некоторых специально категоризуемых групп служит цели их подготовки к выполнению в определенных контекстах роли протестного и даже, взрывчатого материала, всегда готового к возмущению, к бунтам, к агрессии в случае прямых или имитированных посягательств на их права или привилегии. Очевидно, в нужный момент нетрудно организовать их притеснение или дискриминацию, чтобы данная социальная категория выступила орудием протестов против установившегося порядка. Но и здесь можно пойти еще глубже и обнаружить, что такая искусственная категоризация отдельных групп используется в качестве часовых-дозорных, охраняющих неафишируемые привилегии некоего субъекта, оккупировавшего некую страну как колониальную территорию. Было бы полезно подсчитать количество финансовых учреждений в России и количество работающих там граждан. По предварительным сведениям, их число превышает количество военнослужащих российской армии. А ведь работники финансовых учреждений подчиняются своим глобальным финансовым генералам. Рано или поздно аборигены любой страны начнут прозревать и препятствовать оттоку богатств и результатов их труда в закрома неидентичной им группы. И вот тут и понадобятся средства отвлечения их от коренных нужд и вбрасывание событий, привлекающих внимание к притеснению уязвимых спецгрупп или отдельных категорий животных. К этой рубрике относятся парниковые газы, потепление климата, любые болезни, которыми удастся запугать население. Даже однополые браки имеют свою затененную материальную притягательность. Приемные дети в таких семьях не имеют прав на наследство своих родителей, вследствие чего оно достается банкам. Присовокупите к этим пунктам действующее в России законодательство, по которому, если в течение 6 месяцев после смерти владельца вклада в банк не обратится никто из его родственников, то сумма остается в банке, а не передается государству. Даже служба «Ритуал» не так восторженно встречает смерть, как любой банк. Можно перечислить еще тысячи и тысячи такого рода трюков, подтверждающих полностью искусственный характер современной социальной структуры и гротескную глупость человечества, позволяющего мошенникам насмехаться над ним. Им потакают и выращенные такими же структурами социологи, бегающие с анкетами, вместо того, чтобы помогать людям развенчивать преступные трюки. Это и есть вопиющая дисгармония, осознав которую человечество должно сгореть со стыда. Почему она имеет место? Потому что, вступив хоть раз на стезю обмана и несправедливости, надо постоянно их скрывать, и снова и снова обманывать, утончая связь с жизнью до тонкой ниточки, грозящей оборваться в любой момент. Такие люди – подходящий ресурс для грязных провокаций или усердной агентуры. Чтобы выжить самостоятельно, им необходимо собираться в банды, вступать на путь обмана, который уже не будет осуждаться, т.е., кормиться войной, создавать военно-пиратские организации и, даже государства, и проводить аннексии окружающих территорий. Внутри таких социумов идет обязательное обучение граждан коварству, вероломству, жестокости и беспощадности. Как сказал один из предводителей такого социума: «Плод пощады – раскаяние». Т.е., пощадивший обязательно раскается в своем поступке. Весьма подробное описание таких нравов представлено в нашумевшем турецком фильме «Великолепный век». Очень жалкими выглядят христианские проповеди в таких социумах. Таковы там и все социальные институты. В них предстает своеобразная «Гармония тьмы», которая, в конечном итоге, должна покончить самоубийством. Там ненавидят тех, кого не смогли обмануть. Понимающие это европейские политики изо всех сил поддерживали «умирающую Турцию», которой они вверяли задачу совершения «грязных дел», не желая пачкать свои белые перчатки. Трудно понять постоянные «спасения» Турции со стороны России и щедрую ее подкормку туристами и украинской пшеницей. Утонувшая в двойных стандартах европейская социальная наука вместе с предлагаемой ею категоризацией социальных явлений выступает не столько средством познания, сколько средством закабаления, поскольку для нее первичен импульс самооправдания, а не поиск истины. Но пора перейти к практической реализации перечисленных положений. Пора и социальный мир встраивать в гармоничные отношения. Наука без путей приложения – пустая игра ума. И в то же время, любой предлагаемый ею рецепт и процедуру нужно демонстрировать на их инициаторах. И после подтверждения честности опыта, практиковать его расширенное применение. В чем будет практическое приложение идеальной социальной процедуры, как эталона - точки, воплощающей гармоничную реакцию? Если любой социум рано или поздно придет к ней, то или нужно запастись терпением и суметь прожить долгую жизнь до созревания этого социума, или найти социум-долгожитель и успокоиться в совмещении его и своих ценностей. Т.е., кажущееся большим видимое разнообразие культур и цивилизаций укладывается в целостную иерархию ступеней созревания, на которых они проводят свои века и тысячелетия, пока некий катаклизм не сподвигнет их на одоление подъема к следующей ступени. Пора бы социологии описать и инвентаризировать и эти ступени, систематизировав подъемы и спуски. Тогда ожидаемая таблица народов будет не менее наукоемкой, чем таблица Менделеева. Отсюда возникает другой путь – ускоренная трансформация сознания тех народов, которые уж слишком далеки от идеальной точки. Это приводит нас к понятию «пластилиновых» народов, которых можно лепить по заданному образцу. Помимо естественного взаимовлияния народов еще с древних пор присутствует и намеренное формирование систем ценностей, основополагающих идей и религиозных доктрин одних народов со стороны других. Еще в шумерской литературе описаны дискуссии богов относительно нужных качеств народов, создаваемых для собственного пользования. Профессионалы в отливке нужных форм поведения народов возвели себя в статус жрецов и выделились в качестве обязательного для древних общественных устройств института. Временами они настолько усиливались, что вносили в свои планы создание или разрушение тех или иных империй. В любом социуме присутствуют различные идеологические доктрины. Живя в одном и том же обществе, подчиняясь законам того же государства, люди могут занимать прямо противоположные позиции в судьбоносных для страны событиях, если их мнения опосредованы установкой ближайшей религиозной общины. Патриотизм чаще представляет собой остаток, процеженный через сито религиозных или мировоззренческих доктрин. И в этом плане, прямая обязанность государства - быть на высоте своих идейных позиций, которые не могут быть поколеблены никакими иными доктринами. Но слабость в этом отношении государства создает соблазн индоктринации населения в любом заданном извне направлении. Поэтому и здесь спасение государства - в нахождении идеальной социальной точки. Сегодня стала более дифференцированной и более дробно-специализированной технология создания «нужных» народов и сопутствующих им государств. Появились концепции «служебных народов», подчас специально выведенных и «выдрессированных» под обслуживание конкретных целей в рамках конкретных организационных структур. Чем сильнее организация - тем больше ее персонал предстает служебным народом, и тем более узкие задачи способен он выполнять. Причем, любой проект трансформации народов предусматривает выращивание не только служебной популяции, но и одновременно – ее антагониста, всегда готового вмешаться, когда заартачится первая. Причем, под каждый «служебный народ» выращивается не только внешний, но и внутренний его антипод. Поэтому, как более безопасные, служебные народы выдвигаются на самые высокие посты мировой иерархии. Хотя оттуда особенно видны их ущербность и изношенность. В то время как просто живущим рядом с ними народам продолжают отказывать в образовании и социальном подъеме. Т.е., глобальный мир еще очень далек от правильной иерархии степеней созревания. Есть еще и третий путь – вывести социум на первое место, подчинив ему государство, поставив его по важности на второе место. Это выведет традиционные нормы, обычаи и исповедуемую тысячелетиями общинную мораль на роль регулятора международных отношений. Ведь на чём строится базис отношений людей друг с другом? У народов существуют определённые правила жизни, может быть вообще нигде не записанные, но тем не менее действенные. При этом - очень даже соблюдаемые. Пример – различные кодексы чести, существующие с незапамятных времён, нарушения которых смывались кровью. Понятия совести, справедливости заменяют целые юридические кодексы и не требуют защиты адвокатов. У таких этносов, у которых деградировало, отмерло (атрофировалось) представление о добре и зле, хорошем и плохом – остается только юридическая опора, и тут уже манипуляции законников безграничны. И действительно, в таком случае мы имеем дело буквально с «пластилиновыми» народами, которых лепят под поставленные цели. Люди Запада, привыкнув к главенству официального юридического закона, воспринимают своих законодателей как неотъемлемую часть народа, как членов своей семьи, а законы в их глазах, это правила семейного общежития. И если незаметно мигранты займут места законодателей, европейцы по-прежнему будут законопослушно выполнять уже подмененные предписания. В истории есть выстраданное людьми положение. Кто погибает в тяжелые времена в первую очередь? Те люди, у которых не была развита взаимовыручка. Иначе говоря, выручает общинная мораль, обычаи гостеприимства, помощь нуждающимся, соседское взаимосбережение и т.д. Попробуй навредить соседу. Долго не проживешь. Как минимум, переедешь. Отсюда вырастает новое отношение к государству. А нужно ли оно, если социум нашел свою идеальную социальную точку? Управлять социумом может и Совет уважаемых и авторитетных людей и на общественных началах. Ведь моральный пример, гармоничное поведение выше юридического положения. Огромное число пенсионеров могло бы помочь управлению своим жизненным опытом, учитывая нынешнюю волну молодых управленцев. Конечно, эти предложения - не сегодняшнего дня. Но если возвращается древность, доказавшая свою прочность, то пора вернуть и те же до-государственные и безгосударственные социальные формы, но в новом обличье. Ведь большинство социальных утопий (того же Томаса Мора) выросло на базе знакомства с сохранившимися (на территории Передней Азии) традиционными социальными структурами. Тем более, что тогдашние представления прямо опирались на подытожившее древность учение Гермеса, впоследствии хорошо укрытого от последующих поколений. После работ доктора Хаммера и доктора Берга, возникло новое понимание медицины. Медицина помогает каждому стать своим врачом. Точно также новое социальное мышление помогает каждому стать своим государством. И это очень близко коррелирует с его социальной организацией в древности. Тенденции к самоорганизации заложены в природе, и рано или поздно они завоюют и всю социальную сферу. Если организм - наиболее совершенный образец такой самоорганизации и гармонии, то социальный организм, к которому стремится гармоничный социум явит собой новый продукт эволюции. В самоорганизованном социуме порядком управляет не эгоистичный интерес индивида, а совместная ответственность, пронизанная общей заботой о Целом. Если лечение и учение - услуги, то чем больше будет оказано таких услуг, тем более богаты врачи и учителя, и довольно государство, получающее свою мзду. Но утерян смысл их деятельности. Зачем они работают? Их функция в социуме – сохранять здоровье граждан, а не уговаривать их лечиться. Миссия врача в социуме – не допускать проникновение болезни. Вот за это он и должен получать свою зарплату. А как только в социуме появился первый больной, его зарплата должна быть урезана, может быть и прекращена, до тех пор, пока больной не вылечится. Таков был социальный порядок в некоторых древних обществах. И врач должен был денно и нощно бдить за здоровьем граждан, не допуская даже ухудшения самочувствия. Но точно также полицейский должен получать зарплату не за то, что он ловит преступников, а за их отсутствие, за поддержание состояния безопасности в социуме. А то в реальности, чем шире преступность, тем богаче полицейские. Так, никогда преступность не исчезнет. А если исходить из интересов социума, то если появилась преступность, тогда они прекращают получать оплату до устранения этих явлений или, по-крайней мере, их оплата должна снизиться. Каково будет тогда их отношение к социуму? Правильно, бережное и предупредительное, как мать относится к ребенку, или жених относится к невесте. В самоорганизованном социуме всякий человек – тот же чиновник, следит за состоянием социального порядка и вмешивается, когда он нарушается. Сегодняшняя многочисленная бюрократия выполняет роль дворцовой армии, обеспечивая начальнику защиту и собирая для него мзду. Население с его запросами - для него только помеха его кутежам и прожиганию жизни. Общественные советы специалистов – сантехников, электриков, строителей, учителей, инженеров и т.д. легко осуществят все запросы населения, если государство спешно не превратит их в мафии и бросит на растерзание населению. Соответственно, наличие социальных знаний у специалистов поможет им преодолеть ожидаемые препятствия. Уродливая структура нынешнего государства построена на лоббировании более сильных, на подстройке законодательства под интересы «принятых в закрытые группы», оспорить которые не представляется возможным. Отсюда вытекает и поставленная образованию цель – приучить к принятию этих отношений как вечных. Любое государство ждет естественный переход на метауровень, повышение социальной сложности и интеллекта (если оно в силах это совершить). Не включать сразу все социальные группы в единое Целое, а для каждой группы дать возможность осознать себя частью более совершенного промежуточного Целого, затем подняться еще на ступеньку к следующей Целостности, а свою роль видеть как самое широкое Целое над всеми Целостностями, не мельча и не приставляя полицейских к каждой семье. Похожая структура осуществлена в Иране, частично в Индии, внимательно наследующих богатство мысли древних. Малый социум, община обладает более жесткими воспитательными функциями, чем все пенитенциарные учреждения. А мы ослабляем ее, ошибочно называя ее традиционализмом. Тем самым мы закрываем пути естественным природным и космическим закономерностям, считая себя сильнее их. В условиях стимулирования гармоничного морального поведения происходит очищение от паразитизма, концентрация социальной энергии на позитивных свершениях, раскрепощение созидательной мысли и осознание необходимости защиты такого социального порядка. А в сегодняшней социальной атмосфере человеческое в человеке увяло. Осталась одна меркантильность, которой сопутствует ложь, покрывательство вредителей и издевательство над моралью. Кумирами бомжей можно назвать выпестованных этой атмосферой культурных деятелей, певцов и музыкантов, каждые полчаса меняющих гражданство. Поэтому все дисгармонии рукотворны. Врач, полицейский, учитель, судья, сантехник, электрик, архитектор и все остальные профессии стали разбойными, стали врагами друг другу. Именно из уродливого социума растет дисгармония, которой нет места в природе. Возможно, не так сильна в природе и борьба противоречий? Может быть она придумана, чтобы оправдать взаимоистребление в социуме? Исследования Р.Фолля по акупунктуре показывают, что органы в человеческом организме взаимосотрудничают и отдают свою энергию в помощь ослабленным органам. Циркулирует принцип: «Останови сильного, помоги слабому». В социальном организме эта степень сплоченности пока не достигнута. Между «пластилиновыми» служебными народами невозможны согласованность, а только инструментальная пригнанность. Если один народ веками выращивался как антипод и конвоир другому народу, то вряд ли возможны какие-либо иные отношения, пока оба народа не обретут суверенное право решения своих вопросов. В принципе очень мало самостоятельных народов. Но они действуют по общим для них правилам. Они будут ближе к гармоничным решениям, нежели иные. И совсем никуда не годятся колонизованные народы. Они до мозга костей пропитаны навязанной ролью, которую играют, даже не осознавая своей дрессуры. Их манера принятия решений и общая этика ничем не отличается от пиратского подполья. Внешне они должны выглядеть послушными, а внутри – резать друг друга за косточку. Им десятки раз меняют религию, моральные ценности, «элиты», международных друзей и направления общественной жизни. С ними играют на страхах людей, говорят им, что единственный способ выжить — это объединиться с чем-то или кем-то более сильным, следить за настроениями доминирующих субъектов и т.д. Разделение не столько навязывается сверху, а сколько используется теми, кто видит, куда дует ветер, и раздувает его; тогда каждый человек спешит попасть в коалиции разных там «спасателей». И все это из-за отсутствия понимания существования единственно возможной спасительной линии поведения – придерживаться гармонической Золотой пропорции. В таком случае, теряет свою силу партийность, сам сакраментальный лозунг: «Объединяйтесь!» оказывается слепым. Возникает вопрос: объединяться во имя чего и против чего? Определять себя надо не по отношению к другим, а через создание общего дела. Которое не требует наличия категории «Они». «Мы против Них». «Кто виноват в наших проблемах? Конечно, «Они»!» Кто ненавидит нас и хочет забрать то, что принадлежит нам? «Они»! Исключительно, анти-гермесианская позиция, разрушающая Целое! Возвращаясь к Флоренскому, скажем его словами: «Золотое сечение есть закон ОНТОЛОГИЧЕСКИЙ, и именно, как уяснено ранее, выражает строение ЦЕЛОГО как такового. Этим устанавливается смысл занимающего нас закона» (3, с. 485). Литература 1. Сергиенко П.Я. Триалектика как высшая ступень диалектического развития общества. / «Академия Тринитаризма», М., Эл № 77-6567, публ.27741, 28.03.2022 2. Сергиенко П.Я. Метагеометрия гармоничного мироустройства. LAP LAMBERT Academic Publishing, 2015, - 109 с. ISBN: 978-3-659-70976-0. 3. Флоренский П.А. Сочинения. В 4 т. Т. 3 (1): У водоразделов мысли. М.: Мысль, 1999. 4. Кирий В. Г. О золотом сечении и гармонии в амбивалентных системах. ЖУРНАЛ Вестник Иркутского государственного технического университета №3 (50), 2011 - с.232-241. https://cyberleninka.ru/article/n/o-zolotom-sechenii-i-garmonii-v-ambivalentnyh-sistem ah 5. Златеев Б.С. О применении закона золотого сечения к историческому процессу. ЖУРНАЛ Космическое мировоззрение — новое мышление XXI века. 2004. - сс.198-200. https://cyberleninka.ru/article/n/o-primenenii-zakona-zolotogo-secheniya-k-istoricheskomu-protsessu ---------------------------------- Э.Р. Григорьян, Социальные приложения теории гармоничного развития // «Академия Тринитаризма», М., Эл № 77-6567, публ.28064, 13.09.2022 =================================
======================================
ПРОДОЛЖЕНИЕ ДИСКУССИИ в 2015
Хорошо, отложим. Спасибо за пояснения.
Л.С.
------------------------------------------------------------
Лев Михайлович, Вы пишете: «… я так и не нашел ЗАКОН ТВОРЦА у Вас. Если это просто утверждение о гармонии сотворенного ИМ мира – то это очевидно много тысяч лет».
Это утверждают, но не доказывают математически.
Зодиакальный круг 12 созвездий образует замкнутое энергетическое пространство, то есть электромагнитное (световое) поле. Плотность (мощность) этого поля внутри круга не равномерна. Она зависит от отношения расстояний (координат): между созвездиями по кругу и между противоположными созвездиями по прямым линиям движения лучей света. В итоге их пересечения, в круге образуется три гармоничные геометрические фигуры: два квадрата, обозначающие поля гармоничной симметрии, и прямоугольник, обозначающий поле гармоничной асимметрии... Это к началам понимания физических, биологических законов Творца (Космоса) и математического их моделирования… Понять все это не трудно, но Ваша голова занята другими мыслями и нет времени. Оставим до благоприятных времен.
С пожеланием гармонии своего Я =Петр Сергиенко= 06/06/15
------------------------------------------------------------
Уважаемый Петр Якубович! Большое спасибо за ваши теплые слова и желание помочь мне и науке социальной гармонии! Я попытался вникнуть в Ваш рекомендованный текст, но понял, что он мне недоступен. Во-первых, потому что касается астрономии и математики, в которых я не сведущ. И причем тут Зодиак? Во-вторых, стиль Вашего изложения таков, что невозможно докопаться до сути – я так и не нашел ЗАКОН ТВОРЦА у Вас. Если это просто утверждение о гармонии сотворенного ИМ мира – то это очевидно много тысяч лет. Все мои работы по социальной гармонии соответствуют этой идее, которая повторяется у меня десятки раз. А вот структуратики, механики, динамики и генетики гармонии, особенно социальной, практически нет – они начинаются с МОИХ, в течение почти 40 лет, работ, перед которыми ВСЕ пасуют, а потому отрицают и хулят, вместо того чтобы поучиться и вникнуть. В-третьих, у меня нет времени, чтобы вникать (значит, учиться) принципиально новым для меня вещам Вашей математики, так как я предельно занят нашей Наукой глобального мира, которую я ДОЛЖЕН закончить в текущем году на английском языке. Если бы Вы прислали мне ВЫВОД-ЗАКОН из Вашей работы на 1 стр., Вы бы облегчили мою участь. А вообще с Вашим текстом, в части гармонии, я практически полностью согласен. По причине дефицита времени я вынужден заморозить и отложить нашу дискуссию на год. Если Бог даст время и силы, то через год предлагаю найти месяц, по крайней мере, для взаимного обучения (Вашей математики и моей социологии гармонии) где-нибудь на общей территории – у Вас или у меня. Но это обсудим в следующем году. Я – готов учиться, а Вы? Еще раз спасибо, с уважением, Лев Семашко,
06/06/15 PS. Посылаю это письмо также нашему общему заинтересованному другу - Юрию Цымбалисту - надеюсь, Вы не против. ----------------------------------------------------------------
Уважаемый Лев Михайлович!
Я искренне ценю Вас за несравненный труд подвижничества к всеобщему миру и гармонии на Земле. Вы знаете, что я стремился создать модель математического алгоритма тетрасоциологии. Возможно, это стремление было замечено Творцом и его вектор был направлен на познание мной гармонии математической модели замкнутого энергетического пространства нашей "малой Вселенной", создаваемого 12 созвездиями Зодиакального круга, как части звездной иерархии "большой Вселенной". Прочтите текст http://www.trinitas.ru/rus/doc/0016/001c/00161914.htm и Вы поймете замысел (ЗАКОН) Творца, что ожидает цивилизацию Земли в будущем и какие ее действия должны быть, чтобы СПАСТИСЬ.
Ваша жизнь, вектор труда и организаторских способностей действуют в нужном Творцу направлении, но не опираются на Его ЗАКОН всеобщей гармонизации, в приближенно 4000 годичное пространство которого вошла наша Земля. Возьмите в основу своей деятельности факт первичности этого ЗАКОНА и подчинения ему не созданной математической модели сферонов тетрасоциологии.
Пётр Сергиенко. 05.6.15.
------------------------------------------------------------
Уважаемый Петр Якубович!
Спасибо за отклик. Но реального стремления магов к социуму я не вижу и каких-либо фактов движения к нему Вы не предоставили. Согласитесь, это для Вас TERRA INCOGNITO или неприступная крепость.
С уважением,
Лев Семашко
5 июня 2015
-----------------------------------------------------
Уважаемый Лев Михайлович!
Благодарю Вас за поздравление по случаю публикации моей книги «Метагеометрия гармоничного мироустройства». Поздравляя, Вы делаете упрек математикам Стахову, Сороко, Боднару, Харитонову, Сергиенко и др., развивающим теорию «математики гармонии» (МГ, мг), и даже Г.Перельману в том, что мы не сумели ее применить к Вашей тетрасоциологической теории.
Вы упрекаете меня в том, что я, начав сотрудничество с Вами, прекратил его. И спрашиваете: «Как Вы думаете, будет ли когда-либо переход вашей математики (в варианте либо арифметики, либо геометрии) гармонии за этот, пока непреодолимый рубеж для нее? Есть ли у нее способность и порох для этого? Или нужна принципиально новая ТЕТРАМАТЕМАТИКА гармонии, которая выдвигается мною очень давно, особенно в Азбуке гармонии?» Длительное время мы вели обстоятельную дискуссию.
В своем критическом резюме по завершению дискуссии к 2011 г. на сайте ГСГ http://www.peacefromharmony.org/?cat=ru_c&key=488 Вы пишете: «Дискуссия по мг показала, что маги, будучи на 98% технарями, совершенно не понимают азбуки социальной гармонии, ее тетрарного алфавита, раскрытого впервые в тетрасоциологии, в чем откровенно признался Стахов. Они, как правило, не считают социологию наукой. Поэтому они бессильны в расширении мг на общество. Поэтому они неспособны даже поставить задачу, не говоря уже о том, чтобы ее решить. Моя постановка задачи представлена в письме Г.Перельману… Поэтому главная причина «странности» наших дискуссий (а они начались с 2008 года), их безрезультатности, граничащей с бессмысленностью, является, по моему глубокому убеждению, незнание, т.е. невежество, магов в азбуке социальной гармонии. Без ее знания не может быть никакой серьезной речи и достойной дискуссии по расширению мг на социальную гармонию, на общество в целом, на социологию. Это главный предмет моего критического резюме, которому оно посвящено».
Замечу, Э.М.Сороко – философ, А.С.Харитонов – преподаватель социальных наук, я – в прошлом, преподаватель философии и каждый из нас имеет техническое и математическое образование. Только А.П.Стахов – как бы чистый технарь.
Вы в книге «Азбука гармонии» даете определение: «Тетраматематика – это математика сферных матриц элементов гармонии на основе их фрактального подобия. Она необходима для количественного выражения гармоничных пропорций ресурсов ЛИОВ в любой вариации, число которых в социальном мире бесконечно. Тетраматематика гармонии обеспечивает решение 53 задач гармонизации сферных показателей любых социальных процессов. Она еще не создана, но имеет немало попыток приближения к ней [3, 222–225; 11, 316– 329; 13, 237–242; 17; 18; 19; 20; 21 и др.]. По нашему мнению, наиболее перспек# тивен фрактальный подход».
Вы сформулировали ранее неизвестную и не понятную математикам аксиому: «Фракталы социальной гармонии задаются (определяются) аксиомой сферных гармонических пропорций: для каждого установленного числового значения любого элемента/показателя любой сферной матрицы существует гармоническая («золотая») пропорция числовых значений всех других элементов этой матрицы. Или: изменение числового значения любого элемента/показателя любой сферной матрицы ведет к изменению всей гармонической пропорции этой матрицы». Напомню, аксиома в математике – то, что принимается без доказательства, а все остальное доказывается. Например, аксиомы: диагональ прямоугольника больше любой его стороны; наибольшей площадью при равных периметрах разных геометрических фигур обладает круг и т.п. Не один из математиков Вашу «аксиому» без доказательства не примет. Это не аксиома и даже не гипотеза, а ваше предположение, или желание.
Математика наука абстрактная, выражается в уравнениях, формулах, математических моделях, отражающих объективную реальность. В области МГ уже имеется их значительное количество. Чтобы тетрасоциолгия стала научной теорией и будущей человеческой практикой, как теоретик, используйте эти наработки. А если они не подходят к этой теории, создавайте принципиально новую ТЕТРАМАТЕТИКУ гармонии, которая выдвигается Вами очень давно. Например, как сделал это я, чтобы стала признанной триалектика, как наука о гармоничном развитии природы, общества и мышления. Она получила не только широкое признание, но и значительное развитие в теориях многих ученых. Желаю Вам удачи.
=Пётр Сергиенко= 4 июня 2015
---------------------------------------------------------------------
Subject: Математика гармонии в разных вариантах - какая выйдет на социум?
2 июня 2015 г., 13:29 пользователь Leo Semashko <leo.semashko@gmail.com> написал:
Уважаемый Петр Якубович!
Искренне поздравляю Вас с публикацией новой фундаментальной книги по "Метагеометрии гармонии" и желаю Вам здоровья и движения вперед в этом направлении к социальной гармонии.
Был бы Вам очень признателен, если бы Вы прислали мне для знакомства и публикации фрагменты Вашей книги касающиеся применения Вашей геометрии к социальной гармонии? Или Вы также не дошли до нее как и Алексей Стахов?
Вы оба замечательны внутри ваших чистых математик (арифметики и геометрии гармонии), но, к сожалению, я не нахожу ни одного шага у вас за их пределы в область социальных структур и их обобщений, как в Тетрасоциологии. Наши попытки в прошлом сделать СОВМЕСТНЫЕ шаги также ни к чему ни привели (http://peacefromharmony.org/?cat=ru_c&key=373). Вы, кажется, исключили эти работы в этом направлении даже из списка Ваших работ. Как Вы думаете, будет ли когда-либо переход вашей математики (в варианте либо арифметики, либо геометрии) гармонии за этот, пока непреодолимый рубеж для нее? Есть ли у нее способность и порох для этого? Или нужна принципиально новая ТЕТРАМАТЕМАТИКА гармонии, которая выдвигается мною очень давно, особенно в Азбуке гармонии? См. о ней здесь в варианте 2008 г: http://peacefromharmony.org/?cat=ru_c&key=370. См. также наши дискуссии 5-летней давности здесь: http://peacefromharmony.org/?cat=ru_c&key=488 Спасибо за отклик.
С уважением,
Лев Семашко
2 июня 2015
PS. Вот фрагмент письма Стахова из этой дискуссии 2011 года:
Уважаемые Лев Михайлович и Петр Якубович!
Я остаюсь на тех же позициях, что и раньше:
1. Во-первых, я не считаю вариант "Математики Гармонии", разработанной мною, окончательным и бесспорным. И считаю, что она должна развиваться в различных направлениях. В качестве примера такого развития хочу привести замечательную книгу В.А. Бунина "Биоподобие техногенных систем. Математический код метагармонии", Москва, Красанд, 2010, Я бы рекомендовал Петру Якубовичу написать и опубликовать нечто подобное, чтобы можно было предметно судить о его теории фрактальной гармонии. Если эта теория сводится к делению квадрата в "золотом" отношении на четыре части (что 75 лет назад сделано российским архитектором Г.Д. Гриммом), то я возражаю против такой теории. Эта идея применима к архитектуре, но при чем здесь тетрасоциология? Об этом я уже писал. И здесь моя точка зрения совпадает с мнением Льва Михайловича:
"Вы пишите о Вашей "теории фрактальной гармонии", которая триадна по подходу и тетрадна по предмету (тетрарные сферные матрицы). Я публикую все Ваши работы на этот счет, как и работы Стахова и других математиков. Но я не вижу конкретного применения и конкретного решения главной математической задачи тетрасоциологии: задачи математического выражения гармоничных пропорций сферных социальных фракталов"
2. Я рад, что и Лев Михайлович и Петр Якубович приняли на вооружение введенный мною в 1996 г. термин "Математика Гармонии" и не пытаются опровергать мою теорию, в отличие "от различных развязных, «без царя в голове» субъектов" (по выражению Эдуарда Сороко), которые занимаются шельмованием этого научного направления и пытаются опровергнуть "Математику Гармонии" любыми способами, которые не имеют ничего общего с нормами научной этики. Я всегда относился и отношусь с уважением и ко Льву Михайловичу и к Петру Якубовичу. Первый является генератором огромного количества идей, которые я не все воспринимаю, но его энергии можно позавидовать. Петра Якубовича я считаю одним из крупнейших специалистов в области триалектики. Хотя у нас не совпадают точки зрения на развитие "Математики Гармонии", но Петр Якубович в своей критике никогда не опускался до морального уровня "развязных субъектов", и с ним я готов дискутировать на тему "Математики Гармонии" .....
С уважением,
Алексей Стахов
27/01/11
--------------------------------------------------------------- Уважаемые коллеги!По случаю переписки о "презентации проектов", предлагаю информацию о "Русском проекте математики гармонии", теория которого развивалась четверть века и кратко изложена в недавно изданной книге "Метагеометрия гармоничного мироустройства". Теория содержит много принципиально новых (ранее не известных) элементарных математических знаний, необходимых цивилизации в наступившую эпоху ГЛОБАЛЬНОЙ ГАРМОНИЗАЦИИ. Более подробную информацию можно прочесть по ссылке на документ: http://www.trinitas.ru/rus/doc/0016/001d/00162483.htmКнига заказывается через И-магазин и по цене 39-90 евро, что не любому российскому покупателю по карману. В этой связи, чтобы не нарушить свой договор с издательством LAP, желающим я смогу выслать как бы черновой вариант (до правки) книги для личного пользования. А лучше всего полистать публикации на сайте автора http://www.trinitas.ru/rus/doc/avtr/00/0019-00.htm на основе которых написана книга.С пожеланиями гармонии =Петр Сергиенко=30 мая 2015
--------------------------------------------------------------------------------------------------------------------------------------------------
Сергиенко П.Я.
САКРАЛЬНЫЙ ТРЕУГОЛЬНИК ПОРОЖДАЮЩЕЙ МОДЕЛИ ГАРМОНИИ ВСЕГО.
АЛГЕБРАИЧЕСКОЕ И ГЕОМЕТРИЧЕСКОЕ ПОЗНАНИЕ (Тезисы)
Порождающая модель создает мир идей, или высших богов, а эти высшие боги создают космос … и все реально существующее.Платон Сакральный треугольник (т е о р е м а) – трансцендентный, гармоничный прямоугольный треугольник у которого: а) гипотенуза равна произведению катетов; б) квадрат гипотенузы равен сумме квадратов катетов; в) гипотенуза так относится к большему катету, как больший катет – к меньшему;г) треугольник который многократно раз делится на фрактальные треугольники. Данное определение сакрального треугольника сформулировано мной в виде теоремы, доказательство которой осуществлено алгебраическим и геометрическим методами, а так же практическим построением сакрального треугольника. Разумеется, такая информация требует не только математического доказательства, но и аргументированного пояснения. О постижении мной знания данной фундаментальной теоремы, как «порождающей модели» всего по Платону, можно написать большую книгу, но я попытаюсь все изложить в тезисном варианте. Скажу только, что мое познание происходило не в той последовательности, как об этом ниже повествуется. Разумеется, открытию сакрального треугольника предшествовали открытия гармоничных треугольников, переосмысление известных знаний и разные дискуссии. В этой связи я выражаю искреннюю благодарность А.П.Стахову за представленный мне в 2006 году образный рисунок «золотого эллипса» Яна Грежджельского и описание его построения, данное в его книге «Энергетично-геометрический код природы» (1986 г.). Вокруг геометрического содержания этого рисунка между мной и А.П.Стаховым произошла жаркая дискуссия. Она в моем подсознании оставила вопросы к проблеме «порождающей модели» Платона, исследованием которой я тогда уже занимался. Ответы на них я нашел несколько позже.
В согласии с Википедией, трансценде́нтный (прилагательное) (от лат. transcendo — переступать) — философский термин, характеризующий то, что принципиально недоступно опытному познанию или не основано на опыте. Термин «трансцендентный» употреблялся в философии Канта для обозначения таких понятий, как Бог, душа и других. Трансценде́нтное число́ (от лат. transcendere — переходить, превосходить) — это вещественное или комплексное число… Большинство ученых современной цивилизации полагают, что наша Вселенная, включая человека, устроена по принципу предустановленной (сакральной) гармонии. Однако, по причине нашего фрагментарно-утилитарного мышления, законы гармонии до настоящего времени остаются вне понимания и глубокого осмысления. Автор статьи, развивая более четверти века знания о началах триалектического мировоззрения, заложил в его основание древние представления и знания о фундаментальном принципе предустановленной гармонии, который присущ всей Природе. Знание сущности содержания предустановленной (божественной) гармонии с древних времен и до наших дней является сакральным, эзотерическим. Сакральный (от латинского sacralis – священный), обозначение сферы явлений сакральной геометрии пространств, предметов, людей, относящихся к божественному, религиозному, связанных с ними, в отличие от светского, мирского, профанного. Более подробно с толкованием и пониманием сакральной геометрии можно познакомиться насайте «Просветление» http://www.prosvetlenie.org/mystic/1/22.html Эзотерика – то, что не разглашается и передаётся исключительно из уст в уста, экзотерика – опубликованное, доступное для непосвящённых. То есть, знание, тайна которого раскрыта для всеобщего пользования, перестает быть эзотерическим. Эзотерические знания о сакральной геометрии со времен Пифагора и Платона обретали статус экзотерических (научных) в процессе развития математики методом диалектической логики. Диалектический метод и его логика познания действительности также развивались на протяжении многих столетий. Последний, марксистский этап их развития отразился в следующим определении диалектики. Диалектика – наука о всеобщих законах развития природы, общества и мышления. Базисом диалектического познания, как известно, являлась триада Платона и закономерности отношений в ее развитии. Когда в общественном развитии возникла необходимость в гармонизации общественных отношений и отношений между природой и обществом, диалектическая наука перестала удовлетворять потребности дальнейшего развития общества. Потребовалась более совершенная наука. Такой наукой в силу необходимости стала триалектика. Триалектика – наука о всеобщих законах гармоничного развития природы, общества и мышления. То есть, триалектика – это диалектика более глубокого познания законов бытия и развития божественной действительности. А именно, познания законов развития предустановленной гармонии. Истины науки никогда не начинаются для исследователя с чистого незнания и не представляются им в завершенном виде абсолютного знания. Они складываются постепенно, опираясь всегда на предшествующие знания о действительности и о знаниях. Формирование нового знания включает в себя сложный процесс переосмысления имеющегося багажа знаний о действительности, методов и инструментария, посредством которых добывались знания, изобретение новых методов и понятийного инструментария познания действительности. Предшествующим и развиваемым научным фундаментом знаний нашей цивилизации о гармоничной действительности, являются сакральные знания, которыми владели жреческие Мистерии (наследники знаний предшествующей цивилизации). Часть из этих знаний былипереданы нам представителями Мистерий – Гермесом, Пифагором, Платоном и учениями основных религий. Известно, например, что Платон в 46 лет был инициирован в орден жреческой Мистерии в гармоничной пирамиде Хеопса, стоя на священном прямоугольной формы Алтаре богини Исиды размером около 50х30 дюйма. Можно предположить, что размеры Алтаря грубо округлены до целых единиц, а более точные размеры Алтаря – 49,7377х30,7396 дюйма. Тогда отношение сторон Алтаря 49,7377/30,7396 ≈ 1,6180334 – «божественная мера» гармоничных отношений сторон, где отношение диагонали прямоугольника к меньшей его стороне равно 1,1755706 (мера стороны вписанного в тот же круг пятиугольника, что и данный прямоугольник). Разумеется, порядок описания сведений нового знания не всегда совпадает с порядком добывания самого знания. В моих исследованиях, например, чтобы получить новое научное представление о законах гармонии бытия и творении Жизни, потребовалось углубиться в религиозные догматы о Символе Святой Троицы Творца и Его ипостасях.В итоге триалектика автора прижилась в научном познании в более узком смысле (как часть общего учения): Триалектика – наука о началах гармоничного бытия и творения Жизни, в согласии с Символом Святой Троицы Творца, свойствами ее Ипостасей и их математическим моделированием. Любой исследователь знает, что изменения в фундаментальных знаниях неизбежно ведут к переосмыслению всех предшествующих знаний о всеобщих законах. В этой связи есть необходимость очень коротко посвятить читателя в историю о новейшем научном исследовании проблем познания сакральной геометрии и формирования знаний математики гармонии. Математика гармонии – математика, изучающая и моделирующая гармонию бытия пространственно-временных форм Жизни, их количественные отношения, проявляющиеся в эволюции природы, общества и мышления. В последней четверти ХХ века в западных странах и в СССР появилось множество исследователей проблем гармонии бытия, гармоничного развития и их математического моделирования. Особое внимание в этой связи обращает на себя деятельность группы исследователей, входящих в Международный Клуб Золотого Сечения (МКЗС) (http://www.goldensectionclub.net/), который был создан в 2003 году. Основателем и постоянным председателем клуба является доктор технических наук, профессор А.П.Стахов, проживающий в Торонто (Канада). К сожалению, в настоящее время МКЗС навязывает научной общественности цивилизации монопольное право на распространение истины о законах математики гармонии. Это право МКЗС выражается в форме проведения ежегодных международных форумов по проблемам гармонии и ее математическим моделям. При этом руководство МКЗС поступает таким образом, чтобы не допустить на форум идеи, которые не согласуются с идеями его лидеров, о чем будет сказано ниже. Поскольку члены МКЗС связаны своими идеологическими штампами, то и реальные математические модели гармонии они оценивают достаточно «криво» и применяют их на сегодняшний день совершенно неадекватно. В этой связи хочется еще раз напомнить, что нет, и никогда не было, никакого абсолютного права на истину, в т. ч. в развивающейся математике гармонии, когда в достижении истинных знаний параллельно применяются разные методы познания. Я исследовал и развивал параллельно с А.П.Стаховым, Э.М.Сороко и многими другими исследователями нашего времени одну и ту же проблему, проблему математического моделирования структурной гармонии, но с другим подходом к ее началам и другим методом познания. Например, свой метод и принципы познания А.П.Стахов изложил в книге «Сакральная Геометрия и Математика Гармонии. Винница, Изд-во "ITI", 2003», в которой сформулировал цель своего познания: «Создававшаяся в течение многих тысячелетий «Сакральная геометрия» — это путь познания Вселенной и человека». В чем я с ним, абсолютно согласен. Достиг ли он поставленной цели? (Рис) Я полагаю, что этого не произошло. Более того, заявляя о междисциплинарном исследовании данной проблемы, он полностью игнорирует геометрический метод познания сакральных начал математики гармонии, поскольку, как сам признает, не понимает этот метод. Ниже я представляю читателям краткое описание своих исследований и свое понимание логики онтологических начал математики гармонии, уповая на то, что кто-то поймет и откликнется на это своими комментариями. Все исследователи, в том числе и я, начинали свой путь познания заявленной проблемы, базируясь на одних и тех же древних знаниях. Однако, каждый из нас осмысливает и толкует их в меру собственных знаний и логического мышления. Например, А.П.Стахов в этой связи пишет, что «…в геометрии древних особая роль отводилась изучению так называемых «совершенных» или «правильных» геометрических фигур, таких как равносторонний треугольник, квадрат, пентагон, гексагон, декагон, а также таких объемных фигур, как тетраэдр, октаэдр, куб, икосаэдр, додекаэдр, известных под названием «Платоновы Тела» и которые в античной науке выражали «Гармонию Мироздания». Такая нацеленность математической науки очень четко отражена в «Началах» Евклида. По свидетельству Прокла, Евклид был последователем платоновской школы». К такому толкованию древних начал у меня имеются существенные замечания. Во-первых, действительно, в конце 4-го века до н. э. вся математика, в том виде, как она изучалась в школе Платона, была собрана в трудах Евклида, и притом так, что этому суждено было остаться образцом на целые тысячелетия. Пять геометрических тел, перечисленных Стаховым, были открыты пифагорейцами, а возможно, унаследованы ими от жреческих Мистерий. Сам Пифагор был инициирован в египетские, вавилонские, халдейские Мистерии. Геометрия пифагорейцев в основном ограничивалась планиметрией. К пяти симметричным правильным телам пифагорейцев: тетраэдру, кубу, октаэдру, икосаэдру и икосаэдру, Платон добавил сферу, как наиболее совершенную из всех сотворенных и движущихся форм пространства, как абсолютно совершенную меру «порождающей модели» мира идей и самодвижения пространства космоса. «Порождающая модель создает мир идей, или высших богов, а эти высшие боги создают космос с его видимыми богами (небесными светилами) и все отдельные его части… Совокупное действие космических идей и материи создает все реально существующее, в том числе, конечно и человека… его души и тела.» «[Тело космоса] было искусно устроено так, чтобы получать пищу от собственного тления, осуществляя все свои действия и состояния в себе самом и само через себя… Ибо такому телу из семи родов движения он уделил соответствующий род, а именно тот, который ближе всего к уму и разумению. Поэтому он заставил его единообразно вращаться в одном и том же месте, в самом себе, совершая круг за кругом, а остальные шесть родов движения были устранены». (*Остальные шесть родов движений, как объясняется в примечании, – это вперед, назад, направо, налево, вверх и вниз, связанные с развитием деятельности органов живых существ, зависимых от окружающего мира). Таким образом, первичной (шестой) и самой совершенной объемной геометрической фигурой в числе Платоновых тел является сфера (шар), как «порождающая модель» частью которой, в каждом конкретном случае, могут выступать остальные пять фигур. Это четко иллюстрируется Рис.1.
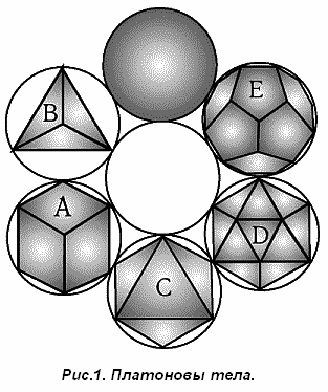
Во-вторых, общей единицей меры геометрических параметров (сторон, периметров, площадей и объемов) шести «Платоновых тел» является радиус сферы (шара, круга), где радиус – мера диаметра (мера вещественного числа).
Я полагаю, что Евклид по какой-то причине обошел онтологический факт, что в круговом движении, присущем всей Природе, в качестве меры отрезка прямой, в согласии с принципомдихотомии целостности, служит диаметр круга. Диаметр круга – дихотомичная целостность двух противоположных радиусов, где мера R = 1. Именно мерой диаметра, а не мерой радиуса измеряется длина окружности и ее отношение к длине диаметра (число π = 3,1415926…). Именно посредством раствора циркуля, круговым движением можно выделить («отсечь») на прямой отрезок прямой, равный двум частям (радиусам) целого и обозначить его пространственную меру числом – 2.Разумеется, при этом раствором циркуля фиксируется так же отрезок радиуса круга, который можно рассматривать как половинную часть целого, пространственная мера которого обозначается числом – 1. Таким образом, онтологически математической мерой дихотомической целостности является не – «1», а – «2». Именно на диаметре круга можно круговыми движениями циркуля построить («отсечь») меру отрезка 1,6180339…, как меру числа, а так же др. числа меньше 2. Радиус кругового вращения является всеобщей естественной мерой всеобщего эллипсоидного движения. Круговое движение – частный случай эллипсоидного движения. Это отмечал и Платон. Круг (окружность) – это эллипс, у которого фокусное расстояние равно нулю. Треугольник – пространственная структура замкнутого двумерного пространства, с минимально возможным количеством сторон, в которую можно вписать и, вокруг которой, можно описать окружность. Треугольник – фундаментальная форма, посредством которой образованы все Платоновы тела, кроме сферы и эллипсоида. В математическом моделировании гармонии следует развивать и синтезировать мировоззренческие и математические идеи начал гармонии Платона (Геометрия есть познание всего сущего) и Пифагора (Все есть число). Пифагор наставлял учеников – узрите треугольник ипроблема на две трети решена. Здесь предполагается в первую очередь «узреть» прямоугольный треугольник, вписанный в круг, где гипотенузой любого треугольника, является диаметр круга и к которому применима теорема Пифагора. В теореме Пифагора четко проявляется принцип гармонии: при пространственном изменении катетов (меры длины и положения), всегда сохраняется неизменной мерапространства гипотенузы. В-третьих, исследователи МКЗС, в математическом моделировании явлений и объектов гармонии, базовым основанием моделирования полагают абстрактнуюмеру мнимой единицы, а не вещественного числа. В результате, для выявления числовой меры «золотой пропорции» (целое так относится к своей большей части, как большая часть относится к меньшей части), эксплуатируется древнее алгебраическое уравнение деления отрезка прямой равного 1 на две не равных части: Х2 – Х – 1 = 0,(1) гдекорни – Х1 = ≈ 1,6180339…; Х1= - ≈ -0,6180339… В итоге решения уравнения, мера части оказывается больше меры целого, чего не может быть в действительности, т.е. не может существовать пространственно. Что явилось причиной получения столь парадоксального результата? Обратимся за ответом к Пифагору. Он учил, что точка символизирует число 1, линия – число 2, плоскость – число 3 и многогранники – число 4. Таким образом, в согласии с Пифагором, отрезок прямой – это линия, мера которой есть число 2, а не – 1. Так было изначально заложено противоречие в составление уравнения (1). Не разрешив данное противоречие (парадокс), многие из исследователей полагают, что число 1,6180339 является не частью отрезка, которую обозначили через Х, а гармоничной («золотой») мерой отношения отрезка равного 1 и его частей, равных 0,6180339 и 0,3819661. Длину мер отрезков 0,6180339 и 0,3819661 вычислил, как известно, Евклид. При этом Евклид геометрически делил на гармоничные части не абстрактный отрезок прямой, а больший катет прямоугольного треугольника, меру которого он принял за 1. При этом мерой деления большего катета равного 1 на гармоничные части он принял меру меньшего катета, который равен половине большего катета, т.е. – меру вещественного числа, где: 1 = 0,6180339 + 0,3819661 и 1/0,6180339 = 0,6180339/0,3819661 = 1,6180339 и 0,6180339/1 = 0,3819661/0,6180339 = 0,6180339. (2) Числовые меры отношения принято обозначать символами: 1,6180339… – Ф; 0,6180339… – ф; ф2 ≈ 0,3819661…;; (3) А.П. Стахов и другие члены МКЗС в математическом моделировании явлений гармонии не учитывают данный онтологический парадокс. За основу комбинаторного моделирования гармонии они приняли числовое равенство: 1 = 1,6180339 х 0,6180339, где 1,6180339 – безразмерное число, а 0,6180339 – часть отрезка. Вещественное число (С) – всеобщая количественная мера половины чего-либо, во взаимодействии противоположностей некой целостности и выражается числами: (4) Вещественное число – одно из самых фундаментальных понятий не только математики, но и всего естествознания. Вещественное число всегда конкретно, а действительное число – абстрактно. В согласии с диалектикой Платона, любое содержание обладает формой, а форма – содержательна. Вещественное число отражает относительное содержание геометрической формы того или иного пространственного объекта или его части. Из этого следует, что меру вещественного числа можно построить геометрически, а геометрию пространственного объекта можно представить в числах мер его параметров и в числах их отношений. Мои исследования математического моделирования числовой гармонии начались фактически с изучения сущности и закономерностей вещественного числа. В конечном итоге, это определило мой, отличный от традиционного, метод познания пространственных форм, количественного содержания и математического моделирования явлений гармонии. В процессе исследований и развития начал математики гармонии мной были сформулированы многие понятия, аксиомы, доказаны теоремы, выведены формулы синтетической и сакральной геометрии триалектики. Гармония – динамическое единство сохранения и изменения бытия чего-либо. Предустановленная гармония – динамическое единство абсолютного сохранения и абсолютного изменения (развития) космоса (Вселенной). Золотая пропорция (ЗП) – отношение целого и его частей, где целое так относится к большей своей части, как большая часть относится к его меньшей части. Золотое сечение (ЗС) – сечение (деление) пространства относительно целостной самостоятельной структуры на две части согласно отношениям золотой пропорции. Пространство при этом может быть одномерным, двухмерным и трехмерным. Оптимальной формой структурной гармонии пространства является треугольник. Определить мерность пространства только по значению того или иного числа вне его геометрической модели, как известно, невозможно. Метод познания и математического моделирования пространственной и количественной (числовой) гармонии осуществлялся автором посредством геометрического моделирования (построения) числовых пространств. В этом принципиальное отличие моего метода познания и моделирования явлений гармонии и развития математики гармонии от метода А.П.Стахова и его последователей. Какими же новыми знаниями в области развития математики гармонии автор триалектики пополнил закрома науки? Я не стану их перечислять все. Любознательному читателю рекомендую полистать статьи, выставленные на сайтах: http://trinitas.ru/rus/doc/avtr/00/0019-00.htm http://www.peacefromharmony.org/?cat=ru_c&key=373http://trialektika.narod.ru/serg.htm и отзывы о триалектике и ее методеhttp://www.trinitas.ru/rus/doc/0016/001c/00161637.htmСогласно содержанию статьи, обращаю внимание читателя на следующие важные начала развиваемой автором математики: ·Применение отличного алгоритма решения древней задачи (Предложение 2.11) от примененного алгоритма решения Предложения 2.11 Евклидом http://www.trinitas.ru/rus/doc/0016/001c/00161570.htm лежащего в основании начал математики гармонии. ·Автор, к известным симметрично гармоничным треугольникам открыл (построил)сакральный гармоничный треугольник и два типа асимметрично гармоничных треугольника, деление их на фрактальные треугольники, что позволяет перейти к математике гармонии многомерных пространств.Построение гармоничных треугольников представлено автором в статьях вышеназванных сайтов. Гармоничный треугольник – прямоугольный треугольник, у которого: а) гипотенуза так относится к большему катету, как больший катет относится к меньшему; б) квадрат гипотенузы равен сумме квадратов катетов; в) треугольник который можно многократно делить на фрактальные треугольники. Гармоничный треугольник является подобием сакрального треугольника. Особого внимания в этой связи заслуживает изучение, так названных автором, «сакрального ромба» и «сакрального треугольника», определение (понятие) которого дано в начале статьи. Данные ромб и треугольник были открыты в построении геометрической модели гармоничного деления биологической яйцеклетки на структурные части. Сущность сакральной (неизвестной) геометрической модели мироустройства многого из единого легче показать и доказать, нежели объяснить ее логику. Сакральное знание о божественном творении гласит: «Мир создан из ничего… В начале было слово, и слово было Бог, и слово было у Бога… Бог создал человека по своему образу и подобию…». Замечу, что в понимании сущности Бога я исповедую философию холизма. Наше знание божественного мы моделируем посредством слов и чисел. Слова состоят из букв, а числа – из цифр. Как известно, в глубокой древности буквы и цифры писались одинаково. Из этого следует, что наши логико-математические модели познания многоуровневой иерархии божественной гармонии мироустройства представляют собой некие формы тавтологии. Заглянем в этой связи в «Новейший философский словарь 2009 г.». «ТАВТОЛОГИЯ (греч. tauto -то же самое; logos -слово) - 1) выражение, повторяющее ранее сказанное в иной языковой форме; 2) Т. в дефиниции - логическая ошибка, заключающаяся в том, что определяемое понятие определяется через него самого, т.е. определяющая часть дефиниции повторяет то, что выражено в определяемой части (»организатор - человек, обладающий организаторскими способностями»); 3) Т. в математической логике - тождественно-истинная (общезначимая) формула, которая при всех исходных наборах значений переменных, входящих в нее, - истинна (например, (А -> В) <-> (A v В) ). Тавтологическая формула образуется из выражающих одинаковую логическую функцию формул с помощью оператора эквивалентности. Логические формулы и соответствующие им высказывания, находящиеся в отношении эквивалентности, взаимозаменяемости Т. следует тавтологичность следующих языковых выражений: «Нельзя начертить треугольник равносторонний, но не равнобедренный» и «Если треугольник не равнобедренный, то он не равносторонний». Т. математической логики являются законами (например, законы де Моргана: (А ^ В) <-> (A v B); (A v B) <-> (А ^ В)». Если сказать коротко об алгебраических уравнениях, то они являются тавтологическими моделями, где левая часть уравнения равна правой, а правая равна «нулю», то есть - «ничего». Вместе с тем они не являются моделями «чистой» тавтологии, поскольку в них всегда присутствует хотя бы одно известное или мнимое число. В уравнениях «чистой» тавтологии нет известных каких-либо числовых величин. Именно таким можно представить уравнение мнимого, сакрального прямоугольного треугольника, у которого гипотенуза равна произведению катетов: Если мы обозначим один катет прямоугольного треугольника символом Х, а другой -, тогда гипотенуза будет равна . А утверждение, что гипотенуза равна произведению катетов, будет иметь тавтологический вид, как абсолютно неизвестная действительность: .(5) Таким образом, изначальным тавтологическим уравнением мнимого сакрального треугольника является уравнение: (6) Теперь напишем уравнение мнимого прямоугольного треугольника, в согласии с теоремой Пифагора (квадрат гипотенузы равен сумме квадратов катетов): (7) В итоге получаем синтетическое уравнение сакрального треугольника: Х3 = Х2 + Хили Х3 – Х2 – Х = 0.(8) Решение уравнения прямоугольного треугольника выявляет единицу меры предустановленной гармонии: Х3 – Х2 – Х = Х(Х2 – Х – 1) = 0,(9) где из решения квадратного уравнения Х2 – Х – 1 = 0 мы находим положительное значение: Х1 = 1,6180339…, то есть – меру большего катета. Меньший катет гипотенуза равна Х1Х2 = 2,0581708. Необходимо сразу понять, что значение корня: Х = 1,6180339… не есть мера «золотого сечения» – Ф = 1,6180339…, а есть мера длины одного из катетов прямоугольного треугольника. И то, что она абсолютно равна числу ЗС, то этот факт является дополнительным свидетельством о многофункциональности данного числа в масштабной гармонии образования множества фрактальных гармоничных структур, происходящих от сакрального треугольника и описываемых изначальным, обобщенным уравнением: Хр = Хр-1 + Хр-2, (10) или Хр – Хр-1 – Хр-2 = 0,(11) где р – целые натуральные числа. Суть тавтологии (комбинаторики) изначального уравнения можно иллюстрировать многими примерами. Например, следующим тавтологическим (комбинаторным) преобразованием: Х7 – Х6 – Х5 = Х7 – 2Х4 – 3Х3 – Х2 = 0, где Х =1,6180339…(12) В этой связи я хочу кратко ознакомить читателя по сути моих теоретических разногласий с А.П.Стаховым. Например, в 2009 г. в статье «Ответ П.Я.Сергиенко» http://trinitas.ru/rus/doc/0232/012a/02322060.htm он пишет: «Обобщенные золотые р-пропорции, введенные мною в книге «Введение в алгоритмическую теорию измерения», затрагивают также основания математики. Я хочу привлечь Ваше внимание к моей статье «Обобщенные золотые сечения и новый подход к геометрическому определению числа», опубликованные в весьма уважаемом «Украинском математическом журнале» (том. 56, 2004 г.) по рекомендации академика Митропольского (хотя для Вас авторитеты не имеют никакого значения). В этой статье вводится новое определение действительного числа, основанного на обобщенных золотых р-пропорциях, которое является обобщением системы счисления Бергмана (р=1). По существу речь идет о новом подходе в теории чисел, в основе которой лежат обобщенные золотые р-пропорции». В указанной статье http://www.trinitas.ru/rus/doc/0232/006a/02320005.htmакадемик Митропольский сообщает: «В 2004 г. «Украинский математический журнал» (№ 8) опубликовал статью А.П. Стахова «Обобщенные Золотые Сечения и новый подход к геометрическому определению числа». В этой статье проф. Стаховым получено ряд математических результатов фундаментального характера, к числу которых относятся: (1) Обобщение задачи о Золотом Сечении. Суть этого обобщения предельно проста. Если задаться неотрицательным целым числом р=0, 1, 2, 3,... и разделить отрезок АВ точкой С в такой пропорции, чтобы было: (13) то мы приходим к алгебраическому уравнению Хp+1 = Хp + 1,(14) корни которого называются обобщенными Золотыми Пропорциями или Золотыми р-пропорциями». А теперь, уважаемый Читатель, сравните мое (составленное от общего к частному) и А.П.Стахова (составленное от частного к общему) уравнения для геометрического определения меры числа: Хр = Хр-1 + Хр-2 (Сергиенко) и Хp+1 = Хp + 1 (Стахов). Любое уравнение, составленное по принципу познания от частного к общему, всегда является уравнением частного порядка, а не общего (обобщенного). Отметим так же, что рекуррентный ряд иррациональных чисел, начинающийся из числа предустановленной меры числа 1,6180339…, так же подобен ряду целых чисел Фибоначчи (1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; …) и выглядит следующим образом: 1,618; 1,618; 3,236; 4,854; 8,09; 12,944; 21,034; 33,978; 55,012; 88,99; 144,002; ..…………………………. Я не буду развивать далее теорию подобия математических начал мира предустановленной гармонии с миром математических начал комбинаторного анализа, а продемонстрирую это на примерах отношений трех типов прямоугольных гармоничных треугольников, построенных мной с помощью циркуля и линейки. Порядок их построения мерой радиуса круга, где R = 1, представлен в моих статьях на персональной странице АТ. Ниже приводятся только параметры вычисленных сторон и площадей, построенных мной треугольников. Рассмотрим в этой связи и проанализируем гармоничные треугольники и их параметры, представленные на Рис.2.
1.Симметрично гармоничные треугольники:
1.1.∆0,1,3 – прямоугольный равнобедренный треугольник, равный четверти вписанного в круг квадрата, у которого: гипотенуза 1-3 = 1,4142135…; катеты 0-1 = 0-3 = 1; квадрат гипотенузы равен сумме квадратов катетов; гипотенуза есть иррациональное число и не равна произведению катетов; … 1.2.∆0,5,6 = ∆1,3,2 – прямоугольные равнобедренные треугольники: ∆1,3,2 – вписанный в круг; ∆0,5,6 – описано-вписанный. Площадь каждого из них равна 1, т.е. – четверти площади квадрата, описанного вокруг круга, и половине площади вписанного в круг квадрата. Сторонытреугольников: гипотенуза 5-6 = 1-2 = 2; катеты 0-5 = 0-6 = 1-3 = 2-3 = 1,4142135…; квадрат гипотенузы равен сумме квадратовкатетов; гипотенуза есть целое число и равна произведению катетов; Данные симметрично гармоничные треугольники можно бесконечно делить на два фрактальных треугольника, которые не наследуют свойство – гипотенуза есть целое число и равна произведению катетов. 2.Асимметрично гармоничные треугольники круга и их параметры: 2.1.∆1,11,2 – прямоугольный треугольник, у которого: гипотенуза 1-2 = 2;
катетытреугольнка: Высота треугольника 11-12 = 0,7861513 = . Отношение сторон: 2.2.∆1,9,2 – прямоугольный треугольник, у которого: гипотенуза 1-2 = 2; катеты 2-9= 1,2360678 = 2ф 1-9= 1,5723028 = 2 . Высота треугольника ; Отношение сторон:
2.3.∆0,11,12 – прямоугольный треугольник, у которого: гипотенуза 0-11= 1; катеты:0-12= 0,6180339 = ф11-12= 0,7861513 = .
Отношение сторон:
Площадь треугольника равна 0,5R2 ≈ 1/8 площади круга. Таким образом, параметры данных типов асимметрично гармоничных прямоугольных треугольников и их отношения выражаются посредством пространственных мер катетов треугольников (геометрических чисел) и чисел их общих мер отношений: 1,6180339… и 0,6180339…, построенных на одной и той же гипотенузе (диаметре круга) равной геометрическому числу 2. Последние два типа треугольниковмы называем гармоничными, поскольку у них гипотенуза так относится к большему катету, как больший катет – к меньшему.
Сакральный треугольник (выделен на Рис.3 красным цветом) равен ¼ части «сакрального ромба», описанного вокруг круга. Он отличается от гармоничного треугольника дополнительным свойством: мера длины его гипотенузы равна произведению длин катетов. Мера длины каждого из катетов – трансцендентное число. Параметры сакрального треугольника (выше по тексту)вычислены автором, как бы посредством алгебраического метода. В действительности все осуществлено наоборот: вначале автор построил сакральный треугольник (что равнозначно – построил числа сакрального треугольника), а потом уже составил на их основании общее уравнение треугольника. Поскольку построение описанного правильного ромба (Рис.3) осуществлялось автором той же мерой раствора циркуля, что и построение описанного квадрата (Рис.2), то мы имеем возможность визуально сравнивать, выделенные красным цветом, треугольники. Площади их кажутся нам почти равными. И это действительно так. Однако, присмотревшись к их сторонам, мы замечаем, что длины у них совершенно разные. В связи с теоретическими претензиями на «обобщение уравнений ЗП и ЗС», я хочу обратить внимание читателя на следующие частные и всеобщие свойства геометрических фигур. Круг – частный случай всеобщей формы эллипса, у которого фокусное расстояние равно нулю. Ромб – симметричная геометрическая фигура с равными сторонами и разными углами между смежными сторонами. Квадрат, – частный случай ромба, у которого стороны равны и углы между смежными сторонами прямые; квадрат – частный случай прямоугольника, у которого стороны равны. Квадрат – симметричная геометрическая фигура, которая при равных периметрах с прямоугольником и ромбом, охватывает самую большую площадь. В круг можно вписать, а вокруг круга можно описать бесконечное множество треугольников. В круг можно вписать, а вокруг круга можно описать квадрат. В эллипс можно вписать, а вокруг эллипса можно описать ромб. В круг можно вписать бесконечное множество прямоугольников. В круг нельзя вписать ромб, но вокруг круга можно описать бесконечное множество ромбов. Площадь красного треугольника на Рис.2 равна 1, а его периметр равен: 1,4142135 + 1,4142135 +2 = 4,828427. Площадь красного треугольника на Рис.3 равна 1,0290854, а его периметр равен 2,0581708 + 1,6180339 + 1,2720196 ≈ 4,9482243. Таким образом, разница в периметрах рассматриваемых треугольников, при почти их равных площадях, составляет: 4,9482243 – 4,828427 ≈ 0,1197973. Данная разница в периметрах треугольников есть число меры энтропии (от ἐντροπία — поворот, превращение), выделяемой или поглощаемой энергии (тепла) при деформациях (пространственных превращениях) квадрата в ромб, а ромба – в квадрат. Возможно, в данном случае мы имеем самый низкий уровень энтропии в допустимых космических структурных преобразованиях одной пространственной формы в другую. Здесь все, как говорится, наглядно, понятно и не требует комментариев. В этой связи я не могу обойти вниманием статью В.Л.Владимирова, А.П.Стахова «Энтропия золотого сечения (раскрыта еще одна тайна золотого сечения)» http://trinitas.ru/rus/doc/0232/009a/02321199.htm В статье, вместо открытия тайны природной простоты, читателю предлагается символьно-числовая комбинаторика, в итоге результатов которой, авторы делают следующие умозаключения: «Но сейчас мы приближаемся к тому, чтобы доказать: не эмерджентность, не резонанс отличают гармоническое золотое сечение от других сечений, а, в первую очередь, энтропия…
Назовем новую пропорцию (4) гармонической, так как в нее входит гармоническое среднее H. Отметим универсальность гармонической пропорции, которая справедлива при любых b≥a>0. Даже при бисекции (b=a) пропорция (4) превращается в тождество 2=2. А при b–0,5H=a, пропорция (4) преобразуется в золотую пропорцию (1). Обозначив разность между «большим» и «меньшим» через d=b–a, из сопоставления (4) и (1) сформулируем основное условие гармонического золотого сечения: b–0,5H=a; d=b–a; d=0,5H. (5) Если разность между «большим» и «меньшим» равна половине гармонического среднего «большего» и «меньшего», то деление целого на «большее» и «меньшее» является золотым гармоническим. Гармоническому золотому сечению соответствует золотая пропорция… Таким образом, гармоническому золотому сечению соответствует максимум энтропии!... Гармоническому золотому сечению, которому соответствует равенство разности d аттракторов и половины их гармонического среднего 0,5Н, отвечает максимальная хаотичность (максимальная энтропия ) процесса суммирования. Таким образом, уравнение гармонического золотого сечения (10) – это среднее арифметическое рекурсий крайних режимов – бисекции и редукции!..» и т.п. Я прошу прощения у Читателя за сделанное отступление, поскольку доказуемое, более убедительно познается в сравнении с чем-то и в чем-то подобным.И еще, чтобы при чтении моей статьи стало возможным визуально ориентироваться в числовых значениях мер параметров геометрических фигур и их пространственных отношениях, рекомендую читателю копировать Рис.2 и Рис.3 на отдельный лист бумаги и положить его перед собой. Рассмотрим параметры геометрических фигур и их числовые отношения, изображенные на Рис.3: Ромб 1,2,3,12: сторона – 2,0581708; диагонали – 3,2360678, 2,5440392; периметр ромба – 8,2326832 равен произведению его диагоналей; площадь (s) – 4,1163416 равна половине периметра (р); отношение площади и диагоналей равно: Ф и . Ромб состоит из четырех сакральных, равновеликих прямоугольных треугольника. Из них можно сложить 2 гармоничных прямоугольникасо сторонами 1,6180339 и 1,2720196, или один гармоничный прямоугольник со сторонами 2,5440392 и 1,6180339. Ромб 10,2,11,12 сторона – 1,6180339; диагонали – 2, 2,5440392; периметр ромба – 6,4721356 не равен произведению его диагоналей;площадь – 2,5440392 не равна половине периметра; отношение площади и диагоналей равно: 1 и . Ромб состоит из четырех гармоничных, равновеликих прямоугольных треугольника. Из них можно сложить 2 гармоничных прямоугольникасо сторонами 1,2720196 и 1, или один гармоничный прямоугольник со сторонами 2 и 1,2720196. Отношения между параметрами ромбов:
Рассмотрим более подробно и наглядно (Рис.3) структурно-фрактальное деление на части, выделенного красным цветом сакрального треугольника, в согласии с его геометрическим определением и алгебраическимуравнением (7): ∆0,1,2 – прямоугольный: р1 ≈ 4,9482243; S 1 ≈ 1,0290854; катеты: 0-1 = 1,6180339 = Ф; 0-2 =1,2720196 = ; гипотенуза 1-2 = 2,0581708 = Ф . Произведение катетов: 1,6180339 х 1,2720196 = 2,0581708 = Ф . Отношения между сторонами: 2,0581708/1,6180339 = 1,6180339/1,2720196 = . Квадрат гипотенузы равен сумме квадратов катетов: 4,2360678 = 2,6180339 + 1,6180339, что соответствует значениям: Ф3 = Ф2 + Ф, или равнозначно уравнениям: Ф3 – Ф2 – Ф = 0 и Ф(Ф2 – Ф – 1) = 0, где решение уравненияФ2 – Ф – 1 = 0 дает нам положительное значение корня ≈ 1,6180339…не зависимо от того, какими символами мы обозначаем неизвестное,Х, У или Ф. ∆0,1,2 многократно делится на фрактальные треугольники. Рассмотрим параметры и отношения параметров тех треугольников, которые обозначены на Рис.3. ∆0,1,4 – прямоугольный: р2 ≈ 3,8900535; S 2 ≈ 0,6360098; катеты: 0-4 = 1; 1-4 ≈ 1,2720196; гипотенуза 0-1 ≈ 1,6180339. Отношение сторон: 1,6180339/1,2720196= 1,2720196/1 ≈ 1,2720196 = . ∆1,4,5 = ∆0,2,4 – прямоугольный: р3 ≈ 3,0581708; S 3 ≈ 0,3930756; катеты: 1-5 = 1; 4-5 ≈ 0,7861513 = ; гипотенуза 1-4 ≈ 1,2720196 = . Отношение сторон: 1,2720196/1 = 1/07861513 ≈ 1,2720196 = . ∆0,4,5 = ∆0,4,6 = ∆0,7,11 – прямоугольный: р4 ≈ 2,4041852; S 4 ≈ 0,242934; катеты: 0-5 ≈ 0,6180339; 4-5 ≈ 0,7861513; гипотенуза 0-4 = 1. Отношение сторон: 1/0,7861513= 0,7861513/0,6180339 ≈ 1,2720196 = . ∆2,4,6 = 0,7,9 – прямоугольный: р5 ≈ 1,8900535; S 5 ≈ 0,1501415; катеты:2-6 ≈ 0,4858683; 4-6 ≈ 0,6180339; гипотенуза 2-4 ≈ 0,7861513. Отношение сторон: 1,6180339/1,2720196= 1,2720196/1 ≈ 1,2720196 = . Отношение периметров прямоугольных треугольников: р1/р2 = р2/р3 = р3/р4 = р4/р5 ≈ 1,2720196 = . Отношение площадей прямоугольных треугольников: s 1/s 2 = s 2/s 3 = s 3/s 4 = s 4/s 5 ≈ 1,6180339 = Ф. ∆0,1,2 делится так же на треугольники: ∆0,2,5; ∆0,2,10; ∆2,5,10; ∆1,2,5; ∆1,2,10, где: ∆0,2,5 – прямоугольный. S 6 ≈ 0,3930756 = 0,5 ; ∆0,2,10 = ∆0,1,4 – прямоугольный. S7 ≈ 0,6360098 = 0,5Ф . Параметры мер и отношений ∆0,2,10, как известно, присутствуют в архитектурномансамбле пирамиды Хеопса. Моя версия математического алгоритма применяемого архитектором в проектировании и строительстве пирамиды Хеопса изложена в статье: http://trinitas.ru/rus/doc/0016/001b/00161302.htm ∆2,5,10 – тупоугольный:S 8 ≈ 0,2429342 = 0,5ф . ∆1,2,5 – тупоугольный. S 9 ≈ 0,6360098 = 0,5Ф . ∆1,2,10 – тупоугольный. S 10 ≈ 0,3930756 = 0,5 . Здесь мы наблюдаем равенство площадей тупоугольных и прямоугольных треугольников: S 6 = S 10; S7 = S 9;S 8 = S 4. Выше уже отмечалось, что в круг, как замкнутую целостную систему, можно вписать бесконечное множество прямоугольников и всего лишь один квадрат, и невозможно вписать в круг ни один ромб. Таким образом, внутренний процесс относительной энтропии количественно (численно) может измеряться между постоянными параметрами вписанного в круг квадрата и разными параметрами множества вписанных в круг прямоугольников. Известно, чем меньше уровень (число) энтропии, тем более динамическая система устойчива и долговечна (живуча). Минимум энтропии присущ гармонично структурированной динамичной системе пространства. Геометрически это моделируется прямоугольниками: 4,8,14,13; 4,8,9,5; 4,6,0,5 (Рис.3), каждый из которых фрактально делится на два и более гармоничных треугольника. Покажем это арифметически. Сравним количественные параметры вписанного в круг квадрата 1,3,2,4 (Рис.2) и вписанного в тот же круг гармоничного прямоугольника 4,8,14,13 (Рис.3): Гармоничный прямоугольник – такой прямоугольник, у которого диагональ так относится к большей стороне, как большая сторона относится к меньшей стороне. Квадрат 1,3,2,4: сторона = 1,4142135…; диагональ = 2; рк = 5,656854…; Sк ≈ 2. Гармоничный прямоугольник 4,8,14,13: стороны 4-8 ≈ 1,2360678; 4-13 ≈ 1,5723026; диагональ 4-14 = 8-13 = 2; 2/1,5723026 = 1,5723026/1,2360678 ≈ 1,2720196 = . рп ≈ 5,6167408;Sп ≈ 1,9434726. Разница между периметрами и площадями данных фигур: рк - рп ≈ 0,0401132;Sк - Sп ≈ 0,0565274 – довольно мала, по сравнению с возможно большой разницей между периметрами 5,656854 – 3,9999999 ≈ 1,6568541 и разницей между площадями 2 – 0,1999999 ≈ 1,8000001. Некоторые члены МКЗС развивают идею математической связи чисел треугольника Паскаля с ЗП, квадрата и прямоугольника с числом ЗС, не вникая в онтологическую (пространственную) сущность меры самих чисел. Например, в статье http://trinitas.ru/rus/doc/0232/009a/02321200.htm «Гиперболические уравнения Золотого Сечения» В.Л. Владимиров и А.П. Стахов вычислили и представляют читателю: «Золотой» прямоугольник М1М2М3М4 (Рис. 3) имеет длину действительной оси…= 2Ф0,5 и длину мнимой оси …= 2Ф–0,5. Его площадь равна 2Ф0,5・2Ф–0,5 =4, то есть тожеравна четырем единицам площади. Отметим также, что у «золотого» прямоугольника М1М2М3М4 длина действительной оси в Ф≈1,618 раз больше длины мнимой оси, то есть, иными словами, у «золотого» прямоугольника (режим ЗС) длина больше высоты в Ф раз». Мы знаем, что квадрат, площадь которого равна 4 кв. ед. – это квадрат, описанный вокруг круга. Прямоугольник описать вокруг круга невозможно. А в круг можно вписать бесконечное множество прямоугольников, но ни один из них не может быть равен описанному квадрату, сторона которого равна 2, а площадь 4. То есть «золотой» прямоугольник – это мнимый прямоугольник. Вычислим отношения между параметрами представленного нам мнимого «золотого» прямоугольника в согласии с данным выше определением гармоничного прямоугольника. Вторая сторона прямоугольника, площадь которого равна 4, а одна сторона равна 1,6180339, вычисляется: 4/1,6180339 ≈ 2,472136, а, согласно теоремы Пифагора, его диагональ ≈ 2,954571. Вычисляем отношения: 2,954571/2,472136 ≈ 1,195149;2,954571/1,6180339 ≈ 1,5278641. То есть 1,195149 ≠ 1,5278641. Как говорится, такой «золотой» прямоугольник и рядом не лежал, с золотом. В этой связи я позволю себе представить несколько гармоничных прямоугольников и их параметры, исходя из числовых мер ихплощадей – 4; 6; 15; 20, где 6; 15; 20 – числа взятые из треугольника Паскаля: ·4: стороны – 1,7733035; 2,255677; диагональ – 2,8692654. Отношения: 2,8692654/2,255677 = 2,255677/1,7733035 ≈ 1,2720196 = . ·6: стороны – 2,1718444; 2,7626288; диагональ – 3,5141179. Отношения: 3,5141179/2,7626288 = 2,7626288/2,1718444 ≈ 1,2720196 = . ·15: стороны – 3,4339875; 4,3680997; диагональ – 5,5563084. Отношения: 5,5563084/4,3680997 = 4,3680997/3,4339875 ≈ 1,2720196 = . ·20: стороны – 3,9652273; 5,043847; диагональ – 6,4158724. Отношения: 6,4158724/5,043847 = 5,043847/3,9652273 ≈ 1,2720196 = . Таких гармоничных прямоугольников существует столько, сколько существует чисел. Каждый из данных гармоничных прямоугольников в свою очередь можно так же многократно раз разделить на фрактальные гармоничные прямоугольники и треугольники. Данные примеры свидетельствуют, что любая мера пространственной действительности, заданная абстрактным числом, может быть преобразована в гармоничную систему числовых и структурно-пространственных отношений, где целое (структура) так относится к большей своей части, как большая часть относится к меньшей части. Заключение. 1.Триединый мир бытия пространственной действительности являет собой иерархическую систему предустановленной гармонии междуцелым и его частями, в котором: ·В иерархической системе мира нет такого целого, которое не являлось бы частью другого целого, большего его. В этом смысле, понятия целое и часть условны. Любую часть мы можем относительно рассматривать как целое, а любое целое – как часть. ·Целое так относится к своей большей части, как большая часть относится к его меньшей части. ·Всеобщей количественной вещественной мерой целого и части является вещественное число (половина части или целого). 2.Всеобщей мерой структурированного пространства предустановленной гармонии является прямоугольный гармоничный треугольник, в котором кроме относительных свойств сторон по теореме Пифагора, присущи еще свойства гармоничных отношений между гипотенузой и катетами. 3.Всеобщим фундаментальным началом предустановленной гармонии структурированного пространства является сакральный треугольник, в котором кроме относительных свойств сторон по теореме Пифагора и свойств гармоничных отношений гипотенузы и катетов, присуще еще свойство равенства гипотенузы произведению катетов. Свойства количественных отношений между сторонами сакрального треугольника являются фундаментальным началом развивающейся божественной математики гармонии. Ценность добытых знаний, как известно, проверяется временем в процессе их развития и использования в практике научно-технического прогресса. Реплика в связи с организацией и проведением в Одессе 21-28 сентября 2011 г. Международного конгресса «Гармоничное развитие систем – третий путь человечества». Идеологи и организаторы данного Форума, как и предыдущего, всячески стремятся не допустить меня с докладом на его пленарном заседании и к проведению занятий с командированными учителями Украины. Это понятно, поскольку предлагаемые мной знания очень понижают научный и нравственный рейтинг идеологов МКЗС и некоторых крупных чиновников от науки. Я не стану публиковать всю мою переписку с руководством Оргкомитета, копии которой были отправлены интересным мне людям. Приведу только последние тексты. Перевод текста на иностранный язык Платная услуга по профессиональному переводу предоставляется компанией Переведем.ру Уважаемый Пётр Якубович!
К сожалению, пока мы не располагаем средствами на оплату, поскольку спонсорская помощь резко сократилась. То, что имеем, в первую очередь, планируем тратить на проведение Конгресса, организацию обучения учителей (преподаватели здесь работают бесплатно) и издания Конгресса.
Ситуация в Украине сейчас экономчески очень и очень сложная и получить дополнительные средства очень трудно. Государственные ВУЗы не принимают участия в финансировании. Затраты прошедшего Конгресса, практически все, также оплачивала коммерческая организация, куда ежегодно просто некоорректно обращаться. Поэтому Ваше условие оплаты проезда, проживания и питания для Организаторов Конгресса, в настоящий момент, является нереальным, хотя мы прекрасно понимаем, что на пенсионные доходы Вам выбраться сложно.
Просим отнестись с пониманием к нашему ответу. Но на сегодняшний день ситуация именно такая.
С уважением,
Заместитель руководителя Оргкомитета Егорова-Гудкова Т.И. Уважаемая Татьяна Игоревна! Благодарю за обстоятельный и довольно лицемерный отказ. Мне понятно еще по прошлогодней переписке, что для Вас, Стахова, Сороко, Боднара и некоторых других – я, как докладчик, на Конгрессе не желательный. В сравнении с перечнем недельных мероприятий Форума и финансовыми затратами на их проведение, оплата моего проезда и проживания в студенческом общежитии не соизмеримо ничтожна, чтобы по поводу ее проводить параллель с экономической ситуацией в Украине. В сложившейся ситуации участники Конгресса и обучение учителей нуждаются больше во мне, как носителе новых знаний, нежели я – в них.Видит Бог, в моей помощи нуждаются, но отказываются от нее. Как говорят украинцы в таких случаях: «Баба з возу на колеса легче». С уважением =Петр Сергиенко= Возможно, данная статья и реплика призовет кого-то стать моим спонсором для моего участия в Форуме (оплатить оргвзнос участника Форума, проезд и проживание). В этой связи я хочу сказать следующее. Спонсор, который ценит мои идеи и знания, может уведомить организаторов Конгресса о своем спонсорстве, предложить, просить или требовать включить меня в число выступающих на пленарных и секционных заседаниях Форума. После согласительного ответа Спонсору организаторами Форума Спонсору, я согласую все остальные проблемы в рабочем порядке. С чувством большой благодарности Спонсору, я буду выполнять свою миссию – передавать людям те знания, что даны мне Богом и осмысленны мной. Полезно будет и то, что на виду общественности Конгресса и СМИ окажется благородный поступок Спонсора. © Сергиенко П.Я., 2011 15 июня 2011 |
-----------------------------------------------------------------------------------------------------------------------------
ДИАЛЕКТИКА, ТРИАЛЕКТИКА, ТЕТРАСОЦИОЛОГИЯ И НАЧАЛА ИХ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ Кто умеет делать, тот делает и учит делать. Кто не умеет делать, но умеет учить,учит. Кто не умеет ни того ни другого, учит тому, как нужно учить (Древняя притча). Первой предпосылкой для написания данной статьи послужила, сформулированная Президентом Глобального Союза Гармонии (ГСГ) Л.М.Семашко задача математизации его теории фрактальной гармоничной тетрасоциологии, которую он полагает не выполненной до настоящего времени. В этой связи оговорюсь о том, что в данной статье ставится ударение не на описании сущностного содержания диалектики, триалектики и тетрасоциологии. Решение такой задачи посильно только отдельной книге. Ударение ставится на описании исключительно НАЧАЛ математического моделирования гармонии. И, в особенности, математического моделирования предустановленной гармонии, идеи которой развивались Пифагором и Платоном, классиками диалектики, а так же в работах автора и получили свое развитие во множестве философских работ Л,М.Семашко. Второй предпосылкой является философская и научная дискуссиямежду многими исследователями, развивающими математику гармонии, в том числе, решающими конкретную задачу, поставленную автором тетрасоциологии, в частности, в документе http://www.peacefromharmony.org/?cat=ru_c&key=488 Третьей предпосылкой является то, что проблема создания математики гармонии вызвана необходимостью дальнейшего развития цивилизации. В ХХ веке развитие производительных сил и НТП общества, как части природы и его общественных отношений, вступило в стадию антагонистических противоречий с предустановленной гармонией, с естественным сохранением природы. Это поставило под сомнение действенность законов диалектики на данной стадии развития общества и потребовало переосмысления ее мировоззренческих и математических начал. «Миру нужна сейчас именно такая математика, чтобы не погибнуть, выжить и подняться на уровень универсальной социальной гармонии как новой, высшей, цивилизации» (Л.М.Семашко). В чем принципиальное отличие от диалектики, пришедших на смену ей новых научных теорий, в частности, триалектики и тетрасоциологии? Диалектическое мышление, познание и знание развивалось тысячи лет. Триалектика и тетрасоциология, зародившиеся в конце ХХ века, так или иначе, базируются на знаниях добытых диалектикой и являются их дальнейшим развитием. Исторически можно выделить несколько типов диалектического мышления и познания истины о действительности: ·Диалектика Сократа, как искусство диалога. ·Античная диалектика: «Все течет, все изменяется (Гераклит); диалектика движения Зенона Элейского; диалектика тождества и различия Платона. Становление античной диалектики заканчивается объективной диалектикой Аристотеля, как учением о противоположностях и методом их познания. ·Идеалистическая диалектика немецкой классической философии (Фихте, Кант, Гегель). ·Материалистическая диалектика эпохи марксизма. Она, по мнению многих, наследовала и развивала фундаментальные идеи всех предшествующих типов диалектического мышления и познания истины о действительности. Классическое ее определение сформулировано Фридрихом Энгельсом. Диалектика – наука о всеобщих законах развития природы, общества и мышления. В конце 80-х годов прошлого века во Франции как бы получило свое возрождение древнее плюралистическое мышление и познание мира посредством триад в трудах профессора Гомеса де ла Вега. Такое мышление и познание он именовал – триалектикой. Будучи бессистемной и альтернативной диалектике, его триалектика не получила достаточного развития, подверглась сильной критике и быстро исчерпала себя. Почти в то же время, не зная ничего об этом, П.Я.Сергиенко, осмысливая и переосмысливая онтологические начала диалектики, продолжил их развитие до нового методологического уровня познания, понимания и образного представления о пространственно-временной картине мира, которому так же дал имя «триалектика».Все это изложено в изданной монографии «Триалектика. Новое понимание мира» (1995), которая позже была переведена на английский язык и помещена в библиотеку Конгресса США. Триалектика – наука о всеобщих законах гармоничного развития природы, общества и мышления. Данное общееопределение ее, как науки, было сформулировано автором после некоторого развития ее математических начал. Из данного определения следует: во-первых, что триалектика является наукой о законах гармоничного развития противоположностей бытия; во-вторых, что триалектика включает в себя также базовые основания, принципы и законы развития диалектики. Базовым основанием системного метода познания истины, как диалектики, так и триалектики, изначально принята триада. Поскольку видов триад (божественных, онтологических, физических, гносеологических, психологических, математических, …) существует множество, то это нашло свое отражение в разных подходах к их составлению, к выявлению разных связей между ними. Следует заметить, что некоторыми авторами группируется и исследуется множество триад, которые не представляют собой триединую (трехипостасную) онтологическую сущность, как некую целостную систему. Как правило, философские концепции, при таком подходе, в своем большинстве не выходят за рамки вульгарного триадизма. Вместе с тем, некоторые из них выступают с претензией называться триалектическими. Триалектика, фундаментальные начала которой развивает автор, представляют собой некий синтетический процесс осмысления и переосмысления начал целостного, монистического восприятия мира Парменидом, Гераклитом, Пифагором, Платоном, Аристотелем, христианскими учениями о Святой Троице Творца, учениямиВед и учениями об Инь и Ян. И в этом смысле триалектика, развиваемая автором,является частным случаем данного выше общего ее определения. Триалектика – наука о началах гармоничного бытия и творения Жизни в согласии с Символом веры в Святую Троицу, с шестью присущими ей свойствами триединства и их математическим моделированием. Таким образом, в классическое определение диалектики к слову развитие добавлено всего лишь одно слово – гармоничное. А как много за ним прибавляется! Диалектика в этой связи приобретает новый метод познания явлений действительности и приобретает новое имя, имя – триалектика. Первая монографическая публикация триалектики была издана тысячным тиражом в 1995 году. В 2002 г. она на страницах АТ была представлена как «составная часть, онтологическое и методологическое основание тринитаризма». http://trinitas.ru/rus/doc/0018/d01/00180001.htm Автор в своих публикациях многократно повторяется, что триалектический метод познания не является абсолютной альтернативой диалектическому методу. Триалектический метод является дальнейшим развитием диалектического метода познания противоположных частей целого, но не раздельно, а в их гармоничном единстве с целым. Подтверждением этому служит рисунок дизайна обложки первой монографии автора. Триалектика предлагает концепцию «торсионного» мироустройства пространства-времени нашей Вселенной, которая является альтернативой парадоксальной (противоречивой) концепции «Взорвавшейся и расширяющейся (подобно мыльному пузырю) Вселенной». На обложке монографии автора изображена геометрическая модель фрактала гармоничной структуры самодвижущегося пространства-времени от электрона до Вселенной включительно. Данный фрактал являет собой геометрическую модель торсиона.

Торсион
– целостное, замкнутое пространство тора, которое являет собой мёбиусный, гармонично движущийся континуум пространства в пространстве, являющий собой единство: вращательного движения, движения кручения и движения изгиба тора. Формула А : В = В : (А + В) символически указывает на то, что торсион, как целое пространство, и его две противоположные части находятся в гармоничных отношениях между собой. Замечу, мне удалось изготовить механическую модель торсиона, которая позволяет представить и понять изначальную простоту движения пространства торсионного фрактала, сложность многомерности этого движения и его математического моделирования. Исходя из того, что любая научная гипотеза о пространственно-временном мироустройстве Жизни и Разума Вселенной базируется на фундаментальных основаниях развития физической науки в целом, я понял – ошибку нужно искать в исходных (отправных) началах познания действительности. А исходные научные начала познания мира, человека и его предназначения в мире, тесно переплетены с религиозными. Философия в древние времена формировалась как единство мудрости и математической точности, как наука наук, как некий единый ствол знания, подобный дереву, от которого произрастает множество ветвей разных научных областей знания, в том числе – математика. В этой связиприжилось мнение о том, что на статус научного знания может претендовать только та область знания, которая моделируется посредством математических законов. Ради истины следует заметить, поскольку марксистско-ленинская философия развивалась, как общая методология количественных и качественных отношений без принципиального математического развития их начал, то она перестала быть наукой и, в конечном итоге выродилась в чистую спекулятивную методологию. Понять предназначение и место методологии может древняя притча, прилагаемая в качестве эпиграфа данной статьи. Аналогично похожая ситуация в наше время сложилась в условиях исследования и развития древних знаний об элементарных началах математики гармонии многочисленными современными авторами разных бумажных и электронных носителей научной информации. В процессе обсуждения образовательного проекта ГСГ "Кафедра Гармоничной Цивилизации для любого университета/колледжа мира" (январь 2011 г.) Л.М. Семашко представил нам свое новейшее обобщенное определение тетрасоциологии: «Тетрасоциология –– плюралистическая четырехмерная наука социальной и индивидуальной гармонии, раскрывающая ее азбуку (20 фундаментальных элементов этой гармонии), ее язык, мышление и мировоззрение в гармоничной цивилизации. Эта наука не требуется индустриальной, отмирающей, цивилизации и ее людям. Поэтому она не может найти признания в этой цивилизации и у людей, полностью приверженных ей, признающих только приоритет и максимизацию прибыли-денег. Она требуется гармоничной цивилизации и ее людям, или людям, способным понять ее неизбежность, признающих приоритет и максимизацию гармонии». Что понимается под плюралистической наукой? Плюрализм предполагает множество различных равноправных, независимых и несводимых друг к другу форм знания и методологий познания (эпистемология) либо форм бытия (онтология). Плюрализм оппонирует монизму. Древние мыслители выдвигали в качестве основы всего сущего такие начала, как земля, вода, воздух, огонь и т.д. В современной социологии распространена концепция множественности социальных факторов, имеющих одинаковое значение в жизни сообщества. Эпистемологический плюрализм, как методологический подход в науке, подчёркивает субъективность знания и его историческую (Поппер) и социальную обусловленность. Плюрализм (философия) // Википедия. – http://ru.wikipedia.org/?oldid=29273737. Понять авторскую идею математизации тетрасоциологии, не возможно без глубокого понимания ее источников. Читая работы Л.М.Семашко, я прихожу к заключению; их философским основанием являются: идеи предустановленной гармонии мира, диалектики и математической теории фракталов Бенуа Мандельброта. Проблема математизации гармонии является ровесницей развития математики в целом. С ней мы встречаемся, читая труды древних (особенно античных) философов и математиков. Математика и философия – это первые ветви раздвоения развивающегося единого дерева истинного знания о бытии мира и его явлениях, мышления о них, познания их всеобщих, общих и частных законов. В этой связи И.Кант, утверждал, что в каждой науке столько истины, сколько в ней математики. А Г.Гегель, утверждал, что кризис философии наступает в период отсутствия у нее своей математической сущности. Это прекрасно усвоил также автор философской гипотезы гармоничного развития общества на базе его тетрасоциологии. Чтобы тетрасоциология обрела статус науки, потребовалась для нее специальная математика фрактальной гармонии, философские идеи которой он представил в своей «Математической теории фракталов социальной гармонии «золотой тетрасоциологии»: «Эта теория является частным случаем предыдущей теории (теории фракталов Бенуа Мандельброта – П.С) [1], на которую накладываются ограничения (требования) гармонических «Золотых» пропорций между всеми числами каждой сферной матрицы в их теоретически бесконечном ряду. Фракталы социальной гармонии задаются (определяются) аксиомой сферных гармонических пропорций: для каждого установленного числового значения любого элемента любой сферной матрицы существует гармоническая («золотая») пропорция числовых значений всех других элементов любой сферной матрицы. Или: изменение числового значения любого элемента любой сферной матрицы ведет к изменению всей гармонической пропорции этой матрицы». Как утверждает Л.М.Семашко: «Теория фракталов нашла интенсивное развитие в теории бесконечной вложенности материи, которую называют также дискретной фрактальной парадигмой. Основные результаты в теории бесконечной вложенности материи были получены в первой пятилетке ХХI века» В октябре 2008 года Л.М.Семашко информирует членов ГСГ о создании группы математиков, согласившихся принять участие в разработке сферной (тетрасоциологической) математики гармонии: Алексей Cтахов, проф. математики, Канада Петр Сергиенко, философ-математик, Россия Эдуард Шульц, к.ф-м.н., математик, СПб, Россия Эдуард Сороко, д-р философии, математик, Белоруссия Олег Боднар, д-р, математик, Украина Вадим Трифанов, к.ф-м.н., математик, СПб, Россия. Смысл поставленной задачи математикам состоял в том, чтобы на основе базовой матрицы 4х4 построить бесконечную иерархическую систему фрактальных гармоничных матриц размерностью: 4х16, 4х64, 4х256 и т.д. Спустя некоторое время Эдуард Шульц, Алексей Стахов, Эдуард Сороко в открытой дискуссии между участниками группы и Львом Семашко высказывают сомнение о возможности выполнения поставленной задачи. Олег Боднар и Вадим Трифанов отмалчиваются. Петр Сергиенко спустя год предложил свое решение: http://www.peacefromharmony.org/?cat=ru_c&key=373(статья «От фрактальной математики гармонии триалектики к фрактальной математике гармонии тетрасоциологии»). Под опубликованным текстом статьи Л.М.Семашко помещает свой отзыв: «Дорогой Петр Якубович! Я восхищаюсь Вашим отношением к задаче и Вашими достижениями… С уважением, Лев Семашко 9февраля 2009». Какой-либо критики на решение П.Я.Сергиенко со стороны названных математиков не последовало. Позже, в изданной книге Л.М.Семашко «"Гармоничная Цивилизация" (СПб, 2009, 264с.) http://www.peacefromharmony.org/?cat=ru_c&key=405мы находим следующий текст: «Нам известна только одна теория обобщенных гармонических («золотых») пропорций, которая создана профессором А.П.Стаховым в рамках развиваемой им «математики гармонии» [16]. Однако, ввиду ограниченности «золотых пропорций» только двумя элементами (числами, отрезками и т.п.) способна ли эта двумерная теория найти применение для выражения четырехмерных фракталов социальной гармонии тетрасоциологии?... В 2008 году предложен принципиально другой подход к построению тетраматематики. Он принадлежит … П.Я. Сергиенко и основан не на двумерных «золотых пропорциях» Фибоначчи, а на гармонии трехмерного геометрического треугольника… На основе своей трехмерной математической теории гармонии П.Я.Сергиенко предлагает определение «индекса сферной гармонии» в «золотой тетрасоциологии» [17] или тетраматематике. Этот индекс есть число, выражающее взаимную зависимость обобщенных гармоничных пропорций всех строчек и всех столбцов любой сферной матрицы…». В возобновившейся вновь дискуссии (январь 2011 г.) на мои замечания Л.М.Семашко отвечает: «Вы пишите о Вашей "теории фрактальной гармонии", которая триадна по подходу и тетрадна по предмету (тетрарные сферные матрицы). Я публикую все Ваши работы на этот счет, как и работы Стахова и других математиков. Но я не вижу конкретного применения и конкретного решения главной математической задачи тетрасоциологии: задачи математического выражения гармоничных пропорций сферных социальных фракталов. (Эта задача сформулирована в листове ГСГ для 1-го Конгресса по Математике Гармонии в Одессе: http://peacefromharmony.org/?cat=ru_c&key=471). Но в Вашей теории я не нашел математических формул и аппарата нахождения (определения) этих пропорций при любом изменении этих фракталов в бесконечном ряду сферных тетрарных матриц размерностью 4 х 4 в степени К, где К – ряд натуральных (а может и не только натуральных) чисел. Где эти формулы и аппарат в Вашей теории? Здесь нужна не менее фундаментальная работа, чем работа Стахова. Поэтому ГСГ принял решение обратиться к математикам мира с предложением решить эту непростую задачу, которая посложнее и несравненно важнее задачи Пуанкаре и тому подобных. Это обращение скоро (в течении 1-2 месяцев) будет предложено членам ГСГ для обсуждения». Чтобы не потерять основную нить дискуссии, я должен обратить внимание читателя на стержень дискуссии и процитировать в этой связи мнение А.П.Стахова: «Уважаемые Лев Михайлович и Петр Якубович! Я остаюсь на тех же позициях, что и раньше:
1. Во-первых, я не считаю вариант "Математики Гармонии", разработанной мною, окончательным и бесспорным. И считаю, что она должна развиваться в различных направлениях. В качестве примера такого развитиия хочу привести замечательную книгу В.А. Бунина "Биоподобие техногенных систем. Математический код метагармонии", Москва, Красанд, 2010, Я бы рекомендовал Петру Якубовичу написать и опубликовать нечто подобное, чтобы можно было предметно судить о его теории фрактальной гармонии. Если эта теория сводится к делению квадрата в "золотом" отношении на четыре части (что 75 лет назад сделано российским архитектором Г.Д. Гриммом), то я возражаю против такой теории. Эта идея применима к архитектуре, но при чем здесь тетрасоциология? Об этом я уже писал. И здесь моя точка зрения совпадает с мнением Льва Михайловича». Отвечая А.П.Стахову, Лев Михайлович замечает: «Я присоединил к дискуссии трех профессоров Евгения Абрамяна, Виктора Коноваленко и Генриха Скворцова, причастных к математике, с надеждой, что они обогатят ее идеями новых конструктивных деталей для математики тетрасоциологии, не нарушая, а сохраняя ее добрую атмосферу… Спасибо Вам за указание новой, знаменательной, книги по МГ: В.А. Бунин. Биоподобие техногенных систем. Математический код метагармонии, Москва, Красанд, 2010… Название книги, особенно его вторая часть, очень привлекает… Вызывает сомнения и заявленная трехмерность «любых систем», так как биологический (генетический), социальный и многие другие коды четырехмерны, а не трехмерны… А. Я был бы счастлив признать и согласиться с Вами в том, что Ваша МГ не бинарна, а многомерна, а потому приложима к тетрарным социальным системам, если бы Вы (или любой другой) привели хотя бы один конкретный пример многомерных золотых пропорций из социальной области. К сожалению, я его не нахожу, поэтому мое мнение остается прежним. Буду очень благодарен и высоко оценю, если Вы (или любой другой) дадите такой пример». Далее Л.М.Семашко по пунктам отвечает на вопрос А.П.Стахова: « Я не понимаю, какой мерой связаны четыре фундаментальные объекты тетрасоциологии, например, Люди (Л), Информация (И), Организации (И), Вещи (В)?" Он кратко, по пунктам, раскрывает содержание основных, фундаментальных, качеств ЛИОВ. Меня, с точки зрения фрактальной математики гармонии, заинтересовали прежде всего его суждения об эквивалентах числа, как меры ЛИОВ и, особенно, пункт: «11. Поэтому, единственной мерой социальной гармонии (гармоничных пропорций ЛИОВ и всех их производных на всех уровнях) на переходе от индустриальной к гармоничной цивилизации (т.е. в начале последней) может быть ТОЛЬКО денежное выражение стоимости ЛИОВ и ее производных». «13. ЛИОВ, и ее производные, и их гармония выражаются в статистике матриц их сферных показателей как числовых выражений их стоимости в любой денежной единице, например, триллионы долларов, или любой другой адекватной по масштабу». Таким образом, все выше сказанное Л.М.Семашко о математизации ЛИОВ я привожу к краткому тексту: Формулировка задачи по Л.М.Семашко: На основе базовой матрицы 4х4 требуется построить математическую модель бесконечной иерархической системы, входящих друг в друга фрактальных гармоничных матриц, размерностью: 4х16, 4х64, 4х256 и т.д. Мерой базовой матрицы является некое произвольно взятое число, например, число денег в триллионах, миллиардах, миллионах… долларов, рублей…, гармонично распределяемое между людьми, сферами человеческой деятельности и их составными частями. Полагаю, наиболее яркими и жизненными примерами для составления таких гармоничных моделей может быть, например, число (сумма) денег планируемого бюджета (государства, региона, города, …), общего дохода и их гармоничное числовое распределение согласно матриц 4х16, 4х64, 4х256 и т.д. Пояснения и содержание решения задачи П.Я.Сергиенко: Предположим, нам дано число 2012. Требуется построить образно геометрическую и числовую модель иерархически последовательного деления данного числа (денежного эквивалента пространства ЛИОВ и его производных) на фрактальные части мерами «золотой» пропорции между целым и его частями [2], как указанов задаче. Прежде, чем приступить к решению сформулированной задачи, сделаем некоторые дополнительные пояснения наших допущений и обозначений: ·Исходя из начала предустановленной гармонии, следует, что на гармоничные части может делиться такое целостное пространство, континуум которого изначально устроен гармонично. ·Деление гармоничного пространства, равного числу 2012, включат в себя деление на: фрактальные площади прямоугольников, треугольников, их сторон и гармоничные отношения между ними. ·Для более удобного ориентирования в образном Рис.1, традиционную буквенную систему обозначения точек заменим цифровой, где, например: - отрезок линии между точками 1 и 2 обозначается символом 1-2; - периметр, площадь и объем геометрической фигуры обозначаются точками пересечения сторон и, соответственно символами: Р1,3,5,7…; S1,3,5,7…;V1,3,5,7… ·Доказательство деления на фрактальные и гармоничные части пространства, выраженного мерой числа 2012 (Рис. 1), представляем в таком виде, чтобы любой читатель с калькулятором в руках смог его проверить.  Доказательство 1.Строим и вычисляем гармоничный прямоугольный четырехугольник 1,3,5,7 площадь которого задана числом2012 и его параметрами: стороны1-3 ≈ 39,771052,3-5 ≈ 50,589559; диагональ 3-7 ≈ 64,350912. 2.Делим площадь 1,3,5,7 последовательно на три и на четыре фрактальные гармоничные части, в согласии с мерами иерархического деления ЛИОВ – 4х16, 4х64, 4х256 и т.д., где: ·сумма площадей треугольников – 1006 + 621,74215 + 384,2579 = 2012; ·сумма площадей четырехугольников – 768,51591 + 474,96912 + 293,54668 + 474,96834 =2012. 3..Каждую часть площади после первого деления в свою очередь аналогично делим также на четыре и на три части. В итоге, смежные фрактальные площади, стороны треугольников и прямоугольников оказываются в отношениях, выражаемых посредством констант золотых пропорций, где: Ф ≈ 1,6180339…;ф ≈ 0,6180339…; Чтобы доказать данное утверждение, мы должны осуществить вычисление всех параметров деления площади прямоугольника и их отношений. Параметры фрактального деления прямоугольника 1,3,5,7: 1-2 = 6-7 = 8-9 ≈ 15,191178; 2-3 = 4-9 = 5-6 ≈ 24,579874; 3-4 = 1-8 = 2-9 ≈ 31,266064; 4-5 = 7-8 = 6-9 = 1-18 = 2-17 ≈ 19,323497; 2-8 ≈ 34,76262; 3-9 ≈ 39,772323; 4-6 ≈ 31, 2660128; 7-9 ≈ 24,579857; 2-8 ≈ 34,762613; 4-10 ≈ 19,323519; 5-11 ≈ 15,191212; 6-12 ≈ 11,942581; 1-13 ≈ 13,663191; 2-14 ≈ 19,886161; 2-15 ≈ 12,289937; 2-16 ≈ 15,633032; 3-10 ≈ 24,579862; 9-10 ≈ 15,19123; 9-12 ≈ 15,191214; 7-12 ≈ 9,3886442; 2-13 ≈ 6,6399623; 8-13 ≈ 28,122658; 8-18 ≈ 11,942567; 9-18 ≈ 19,323477; ……………………. Отношения между перпендикулярными сторонами фрактальных прямоугольников: 3-5/1-3 ≈3-4/2-3 ≈4-9/4-5 ≈6-9/6-7 ≈8-9/8-18 ≈ 1-18/1-2 ≈ 14-15/2-15 … ≈ . Отношения между смежными сторонами фрактальных прямоугольников: 2-3/1-2 ≈3-4/4-5 ≈5-6/4-5 ≈5-6/6-7 ≈ 7-8/8-18 … ≈ Ф. Отношения между сторонами каждого из фрактальных треугольников: 3-7/1-7 ≈1-7/1-3 ≈3-9/3-4 ≈3-4/4-9 ≈ 4-6/5-6 ≈5-6/4-5 ≈ 7-9/6-9 ≈6-9/6-7 ≈9-18/8-9 ≈ 8-9/8-18 ≈3-4/3-10 ≈3-10/4-10 ≈4-9/9-10 ≈ 4-5/5-11 ≈5-11/4-11 ≈5-6/6-11 ≈6-11/5-11 ≈6-9/9-12 ≈9-12/6-12 ≈2-14/2-16 ≈ 2-16/14-16 …≈ . Отношения между смежными площадями фрактальных прямоугольников: S2,3,4,9 / S4,5,6,9 = S4,5,6,9 / S6,7,8,9 = S1,2,9,8 / S6,7,8,9 = S2,3,4,9 / S1,2,9,8 = S6,7,8,9 / S8,9,17,18 … ≈ Ф. Числовые значения площадей фрактальных треугольников: S2,3,9 ≈ 384,25795;S3,4,10 ≈ 237,48471;S4,9,10 ≈ 146,77324;S4,9,6 ≈ 237,48456; S5,6,11 ≈ 146,77395;S4,5,11 ≈ 90,71061;S7,8,9 ≈ 146,77334;S6,7,12 ≈ 56,062455; S6,9,12 ≈ 90,71089;S1,2,13 ≈ 45,361536;S1,2,8 ≈ 237,48417;S1,8,13 ≈ 192,12264; S9,8,18 ≈ 90,71083; S2,14,15 ≈S3,14,15 ≈ S2,14,16 ≈ S9,14,16 ≈ 96,064487. Отношения между площадями фрактальных треугольников: S2,3,9 / S3,4,10 ≈ S3,4,10 / S4,9,10 ≈ S4,9,6 / S5,6,11 ≈ S5,6,11 / S4,5,11 ≈ S7,8,9 / S6,9,12 ≈ S6,9,12 / S6,7,12 ≈ S7,8,9 / S9,8,18 … ≈ Ф Таким образом, очевидно, что если мы поделим аналогично первому делению (1х4) каждый из прямоугольников: 1,2,9,8; 2,3,4,9; 4,5,6,9;6,7,8,9на четыре части и т.д., и вычислим отношения их параметров, то мы получим тот результат, который был сформулирован задачей. Аналогично все прямоугольники будут делиться на 3 (4х3) и на 4 (4х4) фрактальных гармоничных треугольника. Очевидно, что фрактальная иерархия отношения противоположностей триалектической (тринарной) системы гармонии базируется на их асимметрии, а фрактальная иерархия отношения противоположностей тернарной системы – на их симметрии.Трансформировать эти закономерности на гармонизацию социальных систем – дело социологов. Отличительная особенность деления на гармоничные части гармоничного прямоугольника от деления на гармоничные части квадрата (Разъяснение на замечание А.П.Стахова) При делении единичного квадрата на гармоничные площади, в согласии с решением «Предложения II.11» НАЧАЛ Евклида, мы получаем: ·два не равных квадрата, которые в свою очередь делятся на фрактально симметричные прямоугольные треугольники с отношением сторон: гипотенуза/катет = 1,4142135; катет/катет = 1 и на два квадрата с отношением сторон 1/1; ·два равновеликих по площади и периметру прямоугольника с отношением сторон равным: 0,6180339/0,3819661 ≈ Ф. Прямоугольник делится на два треугольника с отношением сторон: гипотенуза/катет ≈ 1,1755707; катет/катет ≈ Ф. Данное образное деление, как замечает А.П.Стахов представлено 75 лет назад Г.Д.Гриммом. Думается, оно было известно уже во времена решения «Предложения II.11» методом Евклида. Предыдущее мое решение http://www.peacefromharmony.org/?cat=ru_c&key=373 поставленной задачи Л,М.Семашко, принципиально отличается от решения Г.Д.Гримма. Оно базируется на прямоугольнике почти равновеликом по периметру квадрату, состоящему из 4-х равных прямоугольных треугольника. Отношения сторон в таком треугольнике не равны. А именно:
·гипотенуза/больший катет ≈
·больший катет/меньший катет ≈ Таким образом, внутренние пропорциональные отношения, в построенном мной, не гармоничном прямоугольнике, делимом на фрактальные треугольники и прямоугольники соответствовали ранее поставленной задаче автором тетрасоциологии. В процессе проведенной последней дискуссии Л,М.Семашко усложнил ранее поставленную задачу. Для ее решения потребовалось построить абсолютно гармоничный треугольник, на базе которого построен гармоничный прямоугольник и осуществлено представленное выше решение поставленной задачи. Абсолютно гармоничный треугольник – такой прямоугольный треугольник, у которого гипотенуза так относится к большему катету, как больший катет относится к меньшему катету и который бесконечно может делиться на 2 и 4фрактальные себечасти. Абсолютно гармоничный прямоугольник – такой прямоугольник, у которого диагональ так относится к его большей стороне, как большая сторона относится к меньшей и составляющие его части могут бесконечно делиться на фрактальные себечасти. Мои замечания о дискуссии Харитонов – Семашко http://www.peacefromharmony.org/?cat=ru_c&key=488 Дискуссия велась о приоритетах истинности тринарного и тетрарного методов познания действительности, их математизации и зашла, по мнению Л.М.Семашко, в тупик. Позволю себе цитировать некоторые основные высказывания оппонентов в этой связи. С:У меня давний и большой спор с триадниками: Баранцев и Ко (из Академии Тринитаризма). Но есть не менее значительная группа тетрарщиков, которая, не отвергая триады, показала большую эффективность четверок, идущих от Пифагора. Х: Математика гармонии построена на трехсущностной математике в отличие от известной бинарной математики, тетрадной математики я не знаю. С: одно дело - научные споры и разные подходы, другое дело (если они не отвергают гармонии в принципе) - создание общего видения мировой, социальной и индивидуальной гармонии. Х: Посылаю вам свою статью и готов помочь вам включить начала математики гармонии в цикл ваших лекций. С: Я буду только рад Вашей помощи, если она будет вписана в конструкцию содержательной теории социальной гармонии и не будет ее разрушать. Х: Вы же почему-то настаиваете на тетрасоциологии, пусть так возможна одна их концепций в социологии, но причем тут тетра математика и тетрафракталы? С: Не я настаиваю на тетрасоциологии, а я ТОЛЬКО продолжаю эту традицию, которая заложена в древности и развивалась такими мощными фигурами в социологии и истории прошлого века, как Фернан Бродель, Макс Вебер, Парсонс, Тоффлер, Бурдье и многими другими. Кстати, Э. Сороко - тоже тетрарщик… Позвольте обратить ваше внимание еще раз на 18-ю главу (32 стр) в книге Гармоничная Цивилизация, посвященную тетрафилософии и тетрасоциологии:
http://peacefromharmony.org/?cat=ru_c&key=425 Х:В этой главе нет никакого математического начала тетра математики. есть разумные и спорные утверждения… В гуманитарных науках можно строить различные концепции, в математике есть жесткая логика, чего нет или при каких условиях это может быть. С:Как я понимаю, Вы крайний пифагореец, для которого сначала число, а потом природа и прочее. Я ценю Пифагора, исхожу из его четверки как начале всего (Бог – почему Вы ЭТО игнорируете?), но я умеренный пифагореец и для меня СНАЧАЛА природа, общество и т.л., а ПОТОМ число (и математика) для них… Я не могу судить Вашу работу, т.к. она посвящена числам, а не сущностям, а я не математик и мой предмет – сущности. Я еще раз обращаюсь к Вам как к математику: Вы беретесь за математизацию ТЕТРАСОЦИОЛОГИИ или нет? Способна Ваша математика работать (исчислять) ее сущности? Вот в чем ГЛАВНЫЙ вопрос, а не в том, что мы не понимаем. Х: Для меня, как и многих до меня, сначала истина, описываемая числом , а потом рассуждения о природе… Возвращаемся к главному вопросу мы за гармонию в обществе или за ее неумышленное или умышленное разрушение? Как я понимаю, это была дискуссия, без обиды будет грубо сказано, «чистого» философа с «чистым» математиком, считающих себя приверженцами пифагорейского учения о гармонии, но... Поэтому их дискуссия зашла в тупик. Ни кто не станет из них оспаривать то, что Пифагор и Платон были философами-математиками. Их отличает от «чистых» математиков и философов то, что развивая философские дефиниции описания сущности предустановленной гармонии мира, они параллельно развивали и их математические дефиниции. В этой связи приведу известные тезисные обобщения (аксиомы) из пифагорейского учения. Древние пифагорейские «числа» представляли собой знаки и символы, отражающие законы космогонии и космологии. Например, согласно некоторым фрагментам первоисточников (Теофраст 58 IВ 14; Эврит гл. 45, 2; Аэций В 15; Аристотель В 17 и др.): монада – абсолютное и неделимое; диада – переход в неопределенное (бесконечное, противоречивое, нестойкое); триада – первое равновесие, снятие противоборства диады и осуществление монады в диаде (симметризация, «успокоение» диады); тетрада – уплотнение и развитие триады в телесное, воплощение идеальной устойчивой триады в мир природы, вторичное осуществление монады, осуществление осуществления. И всякое телесное целое оказывается новой монадой, которая «отпочковалась» от исходной первой путем двойного (парного – прим. автора) осуществления. Таким образом диада, триада, тетрада являют собой последовательные качественные ступени эволюции бытия самоорганизующейся троичной и триединой монады. Я являюсь так же современным неопифагорейцем и неоплатоником, основательно осмыслившим и переосмыслившим развиваемые тысячи лет философско-математические тезисы: «Все есть число» (Пифагор); «Геометрия есть познание всего сущего» (Платон). Следуя примеру великих философов-математиков, я стремился развивать дефиниции двух параллельных ветвей созданной мной триалектики. К построенным геометрически Евклидом числам ф и ф2, я добавил к ним (построил геометрически) числа А так же построил два гармоничных треугольника, площадь одного из которых равна четверти круга. Поделил на многие гармоничные части диаметр, периметр и площадь круга. На этих основаниях заложил начала синтетической геометрии гармонии и т.д. и т.п.Что из этого выросло – судить современным и будущим творцам научного знания. Вместе с тем, я не стал, подобно А.Харитонову, оспаривать тетрарную философию Л.М.Семашко, а решил оказать ему требуемую помощь. Он так же нигде не касается в своих работах философских проблем триалектики. Вместе с тем, из Рис.1. очевидно, что треугольник (триада) является более универсальным элементом по отношению к прямоугольнику (тетраде), поскольку он сам делится на 3 и на 4 фрактальные части и посредством треугольников строятся и делятся прямоугольники и другие фигуры. О реплике Л.М.Семашко: «…в Вашей теории я не нашел математических формул и аппарата нахождения (определения) этих пропорций…» Имеется ввиду – «золотых» пропорций. Во-первых, я решал конкретно поставленную Вами первую задачу так, как я ее понял. На этот раз я представил более подробное пояснение к уточненной Вами задаче и мое ее толкование. Если я что-то понял и истолковал не в русле логики автора, прошу дополнительного пояснения. Во-вторых, я не утверждаю того, что создал теорию математики гармонии, хотя в этом направлении, полагаю, сделал не мало. Я занимался фундаментальными началами математики гармонии. Выше доказано, что мои знания работают эффективно. В-третьих, я умею строить числа. Но это не значит, что, прочтя мои монографии и статьи, кому-то быстро удастся по конкретно заданному числу площади построить конкретный гармоничный прямоугольник, даже если он из моих статей знает то, как строится гармоничный прямоугольник по числу. Это моя тайна. Сделанные мной выше (Рис.1) на вид элементарные построения и вычисления, для современного математика являются сакральными (таинственными), но для меня они – обычные научные знания, поскольку они мне известны. Спрашивается, чем мой талант, денежные средства и 15 лет упорного труда, потраченные на овладение этими знаниями и умениями отличаются от таланта и затраченного труда, например, знаменитых артистов, которые за одно свое участие в веселом празднестве богатеев вознаграждаются гонорарами в 10-30 раз больше моей месячной пенсии? Знания, которые добыты мной, могут значительно продвинуть развитие информационных, экономических, экологических, финансовых и пр. систем, плоды которых в первую очередь будут пожинать современные богатеи. Я не говорю о государстве, которое всем и вся служит тем же 5% богатых. На подобных мне у них денег нет. Они полагают, что подобным мне, должно платить государство (95% бедняков, обираемых разжиревшей многочисленной коррумпированной армией чиновников). Современный уровень культуры финансовой системы общества и ее сознания не готов к освоению научных знаний о гармоничном развитии функциональных систем общества и природы. Это смогут освоить и развить будущие поколения. Все нужно начинать с гармоничного образования и воспитания детей. Так должен ли я делиться открыто и безвозмездно своими знаниями, которые, уже в конкретном их применении, могут продвинуть НТП? Я не беру в счет многих тех, кто на триалектической методологии и добытых мной новых знаниях защитили кандидатские и докторские диссертации и как-то повысили свой нищенский материальный уровень человека науки. Многие из них благодарили меня единственным искренним СПАСИБО!. И я им благодарен за это таким же СПАСИБО!!! Благодарными мне будут и те поколения, которые в будущем будут иметь возможность овладевать уже с 5-го класса началами математики гармонии посредством творческого геометрического построения чисел, методику которого я изложил во многих своих работах. И, даже если я не поделюсь своими секретами, образование, полученное на базе развитых мной начал математики гармонии, позволит им открыть их. Но это будет уже совсем другое общество. В конечном итоге, думается, я заслуживаю того, чтобы на памятной мне доске была изображена «Модель торсиона предустановленной гармонии единства геоцентрического и гелиоцентрического движения звездных систем нашей Вселенной», которая изображена на обложке первой моей монографии, и – рядом с ней ее математическая формула: где автор полагает: π1 = 3,1415926… - константа для вычисления периметра окружности; π2 = 3,1446054… - константа для вычисления площади окружности. Данная формула отражает гармонию 4-х мерного мира, явления которого более устойчивы и не противоречивы, по сравнению с трехмерным миром. ------------------------------------------------------------- [1] Термин фрактал образован от латинского слова fractus и в переводе означает «состоящий из фрагментов» или «из изломанных частей». Он был предложен Бенуа Мандельбротом в 1975 году для обозначения самоподобных структур. Бенуа Мандельброт (Benoit Mandelbrot) — основатель математической теории фракталов как бесконечно вложенных иерархических (рекурсивных) самоподобных множеств. Рождение фрактальной теории связано с выходом в 1977 году книги Мандельброта «Фрактальная геометрия природы» («The Fractal Geometry of Nature»)… Классификации фракталов. В основном фракталы делят на геометрические, алгебраические и стохастические. Первые две группы образуют детерминированные фракталы, а третья – недетерминированные. [2] «Золотой» пропорцией является такая пропорция количественного деления целого на части, где целое так относится к большей своей части, как большая часть относится к его меньшей части. И – наоборот, меньшая часть так относится к большей части, как большая часть – к целому. © Сергиенко П.Я., 15 февраля 2011 ПУБЛИКАЦИЯ: http://www.peacefromharmony.org/?cat=ru_c&key=373 --------------------------------------------------------------------------------------------------------------
ОТКРЫТОЕ ПИСЬМО А.П. СТАХОВУ Многоуважаемый Алексей Петрович! Из опубликованного проекта Программы, очевидно, что Вы являетесь главным организатором Конгресса в Одессе и докладчиком по его теме будете Вы. Далее планируется 7 тематических секций, на заседаниях которых будут обсуждаться конкретные проблемы, обозначенные в Вашем докладе. Из данного документа, очевидно, что содержание планируемого Конгресса является логическим продолжением содержания Международной конференции «Проблемы Гармонии, Симметрии и Золотого Сечения в Природе, Науке и Искусстве» (Винница, 22-25 октября 2003 г.), на которой Вы были главным докладчиком по теме «Сакральная геометрия и математика». Доклад был опубликован в форме брошюры и в электронном журнале «Академия Тринитаризма» (http://trinitas.ru/rus/doc/0232/004a/02320028.htm). В аннотации к брошюре поясняется: «Особенность брошюры состоит в том, что в ней впервые делается попытка дать интерпретацию основных соотношений «Математики Гармонии» с точки зрения «Сакральной Геометрии» и показать, что эти новые математические результаты могут быть использованы для развития «Сакральной Геометрии». Реакцией на данную статью была моя статья «Триалектика о началах мета-геометрии и математики гармонии», опубликованная в том же журнале (http://trinitas.ru/rus/doc/0016/001a/00160093.htm) 10.06.2004, где содержится следующее замечание: «…в предлагаемых основаниях «математики гармонии» А.П.Стахова, присутствует некая теория чисел и новая теория измерения, но мы не находим в ней основания «сакральной геометрии», отличной от начал Евклидовой геометрии, или какого-либо развития их. Таким образом, я полагаю, что поставленная А.П.Стаховым идея создания «математики гармонии» заслуживает всяческого внимания и поддержки. Однако предложенный им вариант реализации данной идеи, как указано выше, имеет существенные недостатки и не является единственным». Мне потребовалось почти 5 лет научных дискуссий и научных доказательств, чтобы Вы признали, что Ваш вариант познания сакральной геометрии «не является единственным». И этот факт был закреплен в конечном итоге в главном документе международной организации «Глобальный Союз Гармонии» (ГСГ), членом Правления которого Вы являетесь. Документ издан в виде книги "Гармоничная Цивилизация" (СПб, 2009, 264с.) и в электронном виде. В 18 разделе данной книги имеется параграф3.2. Математика тетрасоциологии: Тетраматематика (http://peacefromharmony.org/?cat=ru_c&key=425)В этом параграфе имеется следующая запись:«Нам известна только одна теория обобщенных гармонических («золотых») пропорций, которая создана профессором А.П.Стаховым в рамках развиваемой им «математики гармонии» [16]. Однако, ввиду ограниченности «золотых пропорций» только двумя элементами (числами, отрезками и т.п.) способна ли эта двумерная теория найти применение для выражения четырехмерных фракталов социальной гармонии тетрасоциологии?... В 2008 году предложен принципиально другой подход к построению тетраматематики. Он принадлежит талантливому математику П.Я. Сергиенко и основан не на двумерных «золотых пропорциях» Фибоначчи, а на гармонии трехмерного геометрического треугольника…». Добавлю, что недавно мной было осуществлено «золотое сечение» куба на 8 гармоничных частей, иллюстрацию которого я представил в марте сего года в электронном журнале(http://trinitas.ru/rus/doc/0016/001c/00161619.htm). Вам нет необходимости доказывать, что знания в области сакральной геометрии гармонии имеют исключительно важное значение для математического моделирования экологических, экономических, финансовых, биологических и др. систем, не говоря уже об образовании. Таким образом, имеются все основания включить в Программу тему моего доклада на пленарномзаседании Конгресса: Сергиенко П.Я. «Сакральная геометрия гармонии». С уважением =Пётр Сергиенко= 11 марта 2010
--------------------------------------------------
Дорогой Лев Михайлович! Прошу Вас выставить на мою страницу сайта ГСГ статью «Сакральная геометрия гармонии фракталов», в которой впервые в истории математики иллюстрируется прорыв математики гармонии в трехмерное пространство. В кастрированном содержании эту статью после проволочек выставил В.Ю. Татур на сайте Академии Тринитаризма. =Пётр Сергиенко= 7 марта 2010 ------------------------------------------------
Сергиенко П.Я.
САКРАЛЬНАЯ ГЕОМЕТРИЯ ГАРМОНИИ ФРАКТАЛОВ Сакральная геометрия (от лат. Sacralis -священный, обладающий святостью, признаваемый божественным), как совокупность геометрических представлений древней мифологии и религии о пространственных формах мира и ихпропорциях между целым и его частями, лежащих в основе Жизни, является самым древним (допотопным) знанием о мироустройстве космоса и идеей о гармоничных отношениях общественного бытия. Проблема философского и научного познания сакральной геометрии гармонии пространственного мироустройства и гармонизации общественного бытия проходит красной нитью через всю историю настоящей цивилизации, от знаний жреческих Мистерий, до академических знаний наших дней, до теоретических и практических дел Глобального Союза Гармонии (ГСГ): www.peacefromharmony.org. Как подчеркивается во многих программных документах ГСГ, в эпоху современного ускоренного развития экологического и финансово-экономического кризисов на планете Земля, актуальность гармонизации всего во всем возрастает с каждым днем, поскольку названные кризисы грозят человечеству дисгармонией, а точнее – хаосом всех отношений его бытия. В этой связи, анализируя развитие математических знаний о гармонии мироустройства, нам необходимо иметь в виду, что они являются следствием философских концепций разных эпох. В основе познания автором сакральной геометрии гармонии лежит современная (возрожденная древняя) философская концепция триалектического миропонимания. Принцип гармонии мира предполагает равновесие между неизменностью, сохранением (симметрией) частей целостного мира и одновременно постоянным внутренним изменением, развитием (асимметрией) его частей. Истории известно три мировоззренческих концепции представления и познания сущности мироустройства: Метафизическая концепция полагает бытие мира вечным и неизмененным. Миром правят законы симметрии и равновесия. Идеальной геометрической моделью метафизического бытия является круг. Диалектическая концепция полагает бытие мира постоянно изменяющимся (развивающимся) во времени и пространстве. Миром правят противоречия и асимметрия противоположностей. Идеальной геометрической моделью диалектического бытия является симметрично раскручивающаяся спираль, имеющая начало своего развития. Триалектическая концепция полагает бытие мира вечным, в гармоничном единстве развития и сохранения его целостности. Миром правят в гармоничном единстве законы симметрии и асимметрии. Идеальной геометрической моделью триалектического бытия является замкнутый торсион формы ленты Мёбиуса. Основу знаний жреческих Мистерий о гармонии мироустройства составляли знания сакральной геометрии, которые хранились в глубокой тайне и были уделом только посвященных в них. Знания сакральной геометрии – знания о пространстве, о формах пространственного бытия жизни, их упорядоченности и пропорциональной гармонии. Сакральная геометрия отражается в архитектуре древних и современных храмов. Сложно переоценить культурное значение древних пирамид Египта, Мексики, Индии и Перу. Наиболее выдающимися основателями научных знаний древности, которые были посвящены в знания сакральной геометрии являются древнегреческие философы и математики Пифагор (570 —490 гг. до н. э.) и Платон (428 – 347 до н. э.). Древнее предание свидетельствует, что на входе в платоновскую Академию была помещена надпись «Да не войдёт сюда не знающий геометрии». Жреческие знания сакральной геометрии в качестве священных символов были заимствованы разными религиями мира. Наиболее распространенной в религии является геометрическая фигура креста. Крест (пересечение двух линий или прямоугольников) - сакральный символ жизни. Этот символ произошёл от солярного знака, символизирующего движение Солнца по небесной сфере, где окружность символизирует годовой путь Земли вокруг Солнца. Известны Древнеегипетский крест, Греческий крест, Латинский крест, Православный христианский крест, Свастика и многие другие. Каждый из них имеет свою историю и объяснение его символического содержания. В этой связи обращаю внимание читателя на Латинский крест. Латинским крестом (Crux immissa, Crux capitata) называют такой крест, у которого поперечная линия делится вертикальной пополам, причём поперечная линия находится выше середины вертикальной линии. Обычно он ассоциируется с распятием Иисуса Христа и, таким образом, с христианством в целом. Тайна в отношении длин пересекающихся прямоугольников. Пифагорейское учение передавалось ученикам только из уст в уста. Разглашение знаний вне академии Пифагора каралось вплоть до смертной казни. Пифагорейцы были убеждены, что "книга природы написана на языке математики", как спустя почти два тысячелетия выразил эту мысль Галилей. «О самом учении мы имеем теперь лишь приблизительное представление. Доподлинно известно только одно – сущность всех вещей и основу организации Вселенной Пифагор искал в числах и их гармоничных отношениях. Он учил, что в природе есть две силы. Лучшую он называл Единицею, светом, правостью, равенством, прочностью и стойкостью;… Божественная Единица осуществляет себя лишь посредством Двоицы и, проходя через нее, становится реальной, воплощаясь в Троице, то есть в физическом мире. Проявленный – мир тройственен, и потому Тройка – первое совершенное число, образующее закон вещей и истинный ключ жизни. Вся видимая Вселенная определяется Тройкой, ибо тройка содержит в себе все. Примеров проявления этой троичности огромное количество: … Но все они выходят к Высшей Триаде: божественной Единице, принимающей ее в себя Двоице и родившейся в результате этого Троице. Далее Пифагор вводит понятие священной Тетрады, которое заключало в себе глубокую идею синтеза и развития. Согласно этому учению, Вселенная возникшая под воздействием божественной Единицы, вновь возвращалась и заключалась в ней, образуя живой материальный космос…» [1] Пифагорейцы полагали, что о некотором объекте исследования (в данном случае – о гармонии) можно рассуждать не только в философских понятиях о парах противоположностей или оппозиций, но и в терминах чисел и числовых отношений. Исследования музыкальной гармонии подвигло пифагорейцев на универсальное обобщение всех закономерностей мира, которые можно выразить с помощью чисел и сформулировать свой знаменитый принцип "Все есть число". Таким образом, пифагорейцы выдвинули мысль о гармоничном устройстве всего мира, включая сюда не только природу и человека, но и весь космос. Об этом свидетельствует большинство фрагментов, сохранившихся от пифагорейского учения. Многие, опубликованные Платоном, философские и научные знания являются так же тайными. Он, как и Пифагор, получил их от жреческих Мистерий. Мистерии, по предположению, это знания, унаследованные от предшествующей, погибшей в результате Всемирного потопа, цивилизации атлантов. Опубликованные Платоном сакральные знания имеют не только скрытый (зашифрованный, тайный) смысл, но также содержат искажения, отличия от первоисточников, поскольку передавались от поколения к поколению в устной форме. Энциклопедист по мистицизму и оккультизму Мэнли Палмер Холл в этой связи сообщает нам следующий факт из жизни Платона. «Манускрипт Томаса Тэйлора содержит следующий примечательный отрывок: «Платон был посвящен в Мистерии в возрасте 49 лет. Инициация проходила в одном из подземных залов Великой Пирамиды в Египте. ТАБЛИЧКА ИСИДЫ служила алтарем, и перед ней стоял Божественный Платон и принимал то, что всегда было внутри него, но что Мистерия воспламенила и вырвала из сна. После этого восхождения, через три дня, он был принят Жрецом Пирамиды (Жрец принимал только тех, кто проводил в Великом Зале три дня, прошел три ступени и три измерения), и Платону словесно было дано Высшее Эзотерическое Учение, и каждый раздел сопровождался соответствующим символом. Еще через три месяца пребывания в залах Пирамиды Инициированный Платон был послан в мир делать работу Великого Ордена, как это делали до него Пифагор и Орфей» [2] В системном очерке космологии «Тимей» Платон рассказывает читателю поведанные ему древние, тайные знания о геометрическом и числовом устройстве и законах гармоничного творения космоса. Платон, как бы устами Тимея, сообщает читателю: «[Тело космоса] было искусно устроено так, чтобы получать пищу от собственного тления, осуществляя все свои действия и состояния в себе самом и само через себя… Ибо такому телу из семи родов движения он уделил соответствующий род, а именно тот, который ближе всего к уму и разумению. Поэтому он заставил его единообразно вращаться в одном и том же месте, в самом себе, совершая круг за кругом, а остальные шесть родов движения были устранены» [3]. (*Остальные шесть родов движений, как объясняется в примечании, – это вперед, назад, направо, налево, вверх и вниз, связанные с развитием деятельности органов живых существ, зависимых от окружающего мира). «Итак, нам приходится отдать предпочтение двум треугольникам, как таким, из которых составлено тело огня и (трех) прочих тел: один из них равнобедренный, а другой таков, что в нем квадрат большей стороны в три раза больше квадрата меньшей»[4]. Какиз вращающегося пространстваобразуются названные треугольники, остается тайной до наших дней. Приступая к изложению заявленной темы, мы должны уточнить вопрос: имеет ли гармония какую-либо связь с математикой вообще и с геометрией в частности. Или же она является чисто философской категорией, как утверждают некоторые исследователи. В этой связи уместно процитировать мнение знаменитого философа и математика Рене Декарта (1596 – 1650): «К области математики относятся только те науки, в которых рассматривается либо порядок, либо мера и совершенно не существенно, будут ли это числа, фигуры, звезды, звуки или что-нибудь другое, в чем отыскивается мера. Таким образом, должна существовать некая общая наука, объясняющая все относящееся к порядку и мере, не входя в исследование никаких частных предметов, и эта наука должна называться не иностранным, но старым, уже вошедшим в употребление именем Всеобщей математики»[5]. В Большой Советской Энциклопедии мы находим следующее определение гармонии: «Гармония – соразмерность частей и целого, слияние различных компонентов объекта в единое органическое целое. В гармонии получают внешнее выявление внутренняя упорядоченность и мера бытия». Здесь следует заметить, что, цитируемое выше, математическое понятие гармонии свои истоки берет из сакрального принципа гармоничных отношений между целым и его частями: большая часть целого так относится к его меньшей части, как целое относится к своей большей части. Данную пропорцию некоторые философы и математики древности называли «золотой», а ее геометрическое и алгебраическое решение в последующем получило имя «золотого сечения». В этой связи коротко напомним основной, энциклопедический фрагмент из истории развития математического моделирования гармоничных отношений в системе целого и его частей, в согласии с данным принципом. Впервые математическое моделирование «золотой» пропорции осуществлено в «Началах» Евклида (3-й век до н.э.). Во второй книге «Начал» цитируется формулировка древнего предложения о построении равновеликих квадрата и прямоугольника. Цитируем: «Предложение 2.11. Данную прямую рассечь так, чтобы прямоугольник, заключенный между целой и одним из отрезков, был равен квадрату наоставшемся отрезке». Данное предложение по содержанию, как бы подобного столь же древнему предложению «Построить квадрат равновеликий данному кругу».
Решение «Предложения 2.11» с помощью циркуля и линейки Евклидом и последующими математиками в конечном итоге закрепилось в переиздаваемых энциклопедических источниках в том виде, как это иллюстрирует Рис.1.
Геометрическим построением произвольный отрезок прямой а «рассекается» на части, где АМ = 0,6180339…а, ВМ = 0,3819661…а. В итоге данного построения получены числовые константы гармоничного отношения между целым отрезком и его частями при любом числовом значении отрезка, где - константа – 1,6180339887…а – (целое так относится к большей части, как большая часть относится к меньшей части; - константа – 0,6180339887…а – (меньшая часть так относится к большей части, как большая часть относится к целому). Обычно безразмерные числовые значения данных констант для краткости в описаниях обозначают буквенными символами, где Ф = 1,6180339…, ф =0,6180339… Поскольку данные безразмерные числовые константы отношений (Ф и ф)совпадают с мерными геометрическими значениями отрезков, как числовых корней (х1 = 1,6180339…а, х2 = - 0,6180339…а)при решении алгебраического уравнения: x2– x – 1 = 0, где а = 1 и существует числовая закономерность отношений 1/0,6180339 = 1,6180339, то многие математики в этой связи допускают бессмыслицу в арифметической и алгебраической комбинаторике указанных величин. О свойствах и закономерностях проявления данных констант в математической комбинаторике, о месте и значении их для раскрытия истин в разных областях естествознания, за более чем два тысячелетиянаписано бессчетное количество книг и статей. Фраза «деление отрезка на…» в них повторяется несчетно раз и приводятся примеры деления отрезка и прямоугольника на гармоничные части. Однако, в обозреваемой литературе, например, не встречаются предложения, а тем более – их геометрические исполнения (решения): «Рассечь площадь квадрата на три и более частей, где отношения площади квадрата и его частей выражаются мерами констант гармонии»; «Построить круг равновеликий квадрату»; «Поделить круг на гармоничные части» «Найти алгоритм непрерывного деления прямоугольного треугольника на фрактально-гармоничные части» и др. В процессе развития геометрических идей пифагорейцев, Платона и Евклида, автору посчастливилось приоткрыть некоторые тайны сакральной геометрии гармоничного творения вращающегося в себе космоса. Было осуществлено решение «Предложения 2.11» с помощью циркуля и линейки: http://trinitas.ru/rus/doc/0016/001c/00161570.htm В процессе построения равновеликих квадрата и прямоугольника на отрезке прямой, было выявлено непрерывное деление («сечение») квадрата на фрактальные части в отношениях, выражаемых константами гармонии. Деление квадрата мерой радиуса, вписанного в него круга R = 1, на части в согласии с фундаментальным принципом гармоничных отношений иллюстрируется Рис. 2.

Квадрат размером 2 х 2 = 4 кв.ед. делится на 4 части: на два равных прямоугольника и на два квадрата в отношениях: 4/1,527864 ≈ 1,5278640/0,5835921 ≈ Ф2; 1,5278640/0,9442718 ≈ 0,9442719/0,5835921 ≈ Ф. Соответственно, квадрат 1 х 1 = 1 кв.ед., где мера – R = 0,5, делится на части в отношениях: 1/0,3819661 ≈ 0,3819661/0,1458981 ≈ Ф2; 0,3819661/0,2360679 ≈ 0,2360679/0,1458981 ≈ Ф. Напомним, данный квадрат, как божественная единица (монада) поверхности, в согласии с пифагорейским учением, строился посредством двоицы (дуады) и троицы (триады). Построение Рис.2 выявляет «нулевую» точку отсчета структуризации гармоничных отношений в прямоугольной системе координат для разных геометрических фигур. Это можно иллюстрировать геометрическими построениями Рис.3 и Рис.4. и их конкретными вычислениями, пронумеровавточки пересечения линий. При желании, вычисления читатель может выполнить самостоятельно.
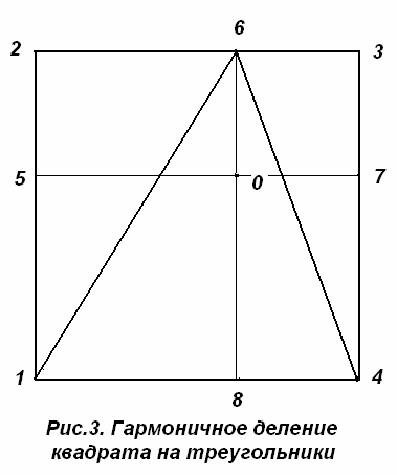
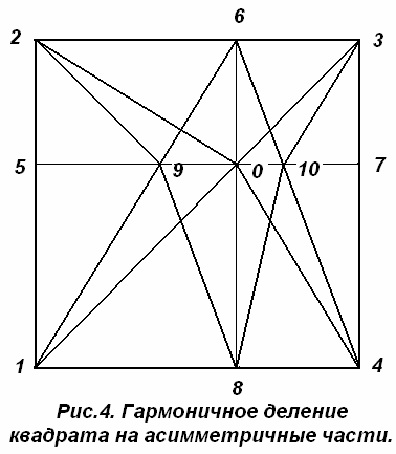
Познав алгоритм «сечения» квадрата на гармоничные части с помощью циркуля и линейки, мы, открываем алгоритм «сечения» на гармоничные части куба (Рис.5). То есть, строим внутренние линии (красный цвет), через которые проходят перпендикулярные плоскости сечения куба. Куб 2 х 2 х 2 = 8 куб.ед. делится на 8 объемных частей (2 куба и 6 параллелепипедов), находящихся в гармоничных отношениях между собой и данным кубом, которые соответственно равны:куб 1,8885432 куб. ед., куб 0,4458248 куб.ед., 3 параллелепипеда по 1,1671848 куб. ед., 3 параллелепипеда по 0,7213592 куб. ед. 1,8885432 + 0,4458248 + 3х1,1671848 + 3х0,7213592 = 8. Отношения между объемами: 8/1,8885432 ≈ 1,8885432/0,4458248 ≈ Ф3; 1,8885432/1,1671848 ≈ 1,1671848/0,7213592 ≈ Ф. Куб объемом 1 х 1 х 1 = 1 куб.ед. делится на 8 объемных частей в гармоничных отношениях между собой и данным кубом, которые равны:куб – 0,2360679 куб.ед., куб – 0,0557281 куб.ед., 3 параллелепипеда по 0,1458981 куб.ед., 3 параллелепипеда по 0,0901699 куб.ед. Отношения между объемами: 1/0,2360679 ≈ 02360679/0,1557281 ≈ Ф3 0,2360679/0,1458981 ≈ 0,1458981/0,0901699 ≈ Ф. Ниже иллюстрируется рисунок выполненный автором только циркулем посредством круговых линий.. На рисунке просматривается как бы куб, вписанный в сферу шара. Этот рисунок как бы наглядно доказывает сакральное утверждение Платона, что космос … из семи родов движения… заставил себя единообразно вращаться в одном и том же месте, в самом себе, совершая круг за кругом, а остальные шесть родов движения были устранены. Автором осуществлено так же «золотое сечение» круга и его периметра [6] непрерывное «золотое сечение» на гармоничные и фрактальные части площадей двух типов прямоугольных треугольников и др.
Таким образом, посредством геометрических построений и вычислений их параметров, мы осуществили переход от«золотого сечения» отрезка на две части – к«золотому сечению» треугольника на две части, квадрата на четыре части, а от него – к «золотому сечению» куба на восемь частей. Заметим при этом, что для осуществления всего этого нам понадобилось всего-навсего знание одной меры – меры радиуса или диаметра круга, выражаемого одним числом. То есть, по одному числу достоверной геометрической меры гармоничной действительности, например, по диаметру атома водорода мы можем просчитать реальные параметры всех систем, которые включают в себя водород.
Copyright © Сергиенко П.Я. --------------------------------------------------------------- 3. Платон. Собр. соч. в 4-х т. «Мысль», М., 1994. Т.3, с.436-437 ---------------------------------------------------------------------------------
От фрактальной математики гармонии триалектики к фрактальной математике гармонии тетрасоциологии Геометрия есть познание ВСЕГО сущего (Платон), а ВСЕ есть ЧИСЛО (Пифагор). О Математическом Проекте «Фракталы социальной гармонии и индекс гармонии в «золотой тетрасоциологии» 25 октября 2008 года Правлением, Консультативным Комитетом и Дирекцией Глобального Союза Гармонии утвержден Математический проект «Фракталы социальной гармонии и индекс гармонии в «золотой тетрасоциологии».Публикация Проекта: на русском языке: http://peacefromharmony.org/?cat=ru_c&key=370 на английском языке: http://peacefromharmony.org/?cat=en_c&key=343 В Проекте изложено содержание параграфов: 1.Историческая и терминологическая справка. 2.Теория социальных фракталов тетрасоциологии. 3.Математическая теория социальных фракталов тетрасоциологии. 4.Математическая теория фракталов социальной гармонии «золотой тетрасоциологии». 5.Индекс сферной гармонии в «золотой тетрасоциологии».
В предложении всем желающим принять участие в данном математическом Проекте так же названы фамилии 6 представителей России, Канады, Украины, Белоруссии, которые имеют научные работы в области теории математики гармонии и которые дали согласие попробовать свои силы в данном Проекте. В дополнение к содержанию 5 параграфов данного Проекта я прилагаю сканеркопии двух рисунков, размещенных на обложке учебного пособия (часть 1) для студентов ВУЗов: Семашко Л.М. Социология для прагматиков. От монизма к тетрализму. «Европейский Дом», Санкт-Петербург, 1999, 376 страниц.
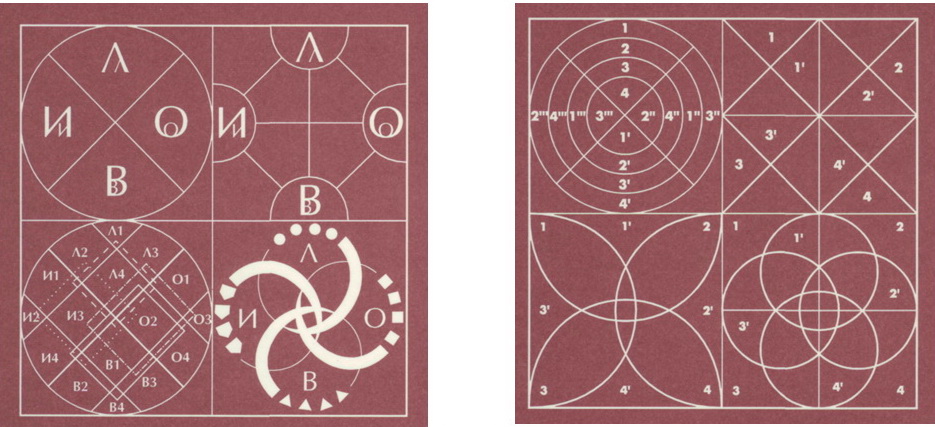
Данные рисунки дают нам образно-геометрическое представление Л.М.Семашко о социальных фракталах тетрасоциологии, которые, в согласии с Проектом, необходимо формализовать в мерах гармонических («золотых») пропорций. Проект содержит пояснение: «Нам известна только одна теория обобщенных гармонических («золотых») пропорций, которая создана А.П.Стаховым [7]. Способна ли эта теория найти применение для выражения фракталов социальной гармонии тетрасоциологии? Это применение было бы мощным, может быть самым значительным, подтверждением и развитием теории Стахова, как и любого другого варианта математики гармонии (МГ). Эта теория была бы революцией не только социальных наук, но и самой математики, которая бы впервые создала математический аппарат, адекватный целостному четырехсферному социуму и целостному четырехмерному социальному пространству-времени. И целостный социум, и целостное социальное пространство-время впервые представлены в тетрасоциологии и ее сферных матрицах [9]. Тетрасоциологическая математика гармонии – это совершенно особый и революционный ее вариант». К данному пояснению следует добавить, что, после нескольких месяцев экспертной работы,А.П.Стахов вынужден был признать ограниченность его теории и неприменимости ее к теории социальных фракталов тетрасоциологии. К аналогичному выводу пришли и другие математики, за исключением П.Я.Сергиенко, который вызвался внести в предложенный проект свой вклад, исходя из тех фундаментальных открытий в области МГ, на которые в 2008 году Федеральным агентством по образованию РФ ему было выдано Свидетельство об отраслевой регистрации разработки «Изначальные алгоритмы элементарной математики гармонии» ОФАП №10170 ВНТИЦ №50200800579.Отраслевой экспертизе были подвергнуты все публикации автора на электронных носителях за период 4-х предшествующих ей лет. Подробнее в http://trinitas.ru/rus/doc/0016/001c/00161462.htm В их числе, также доклад на Международной конференции по проблемам стандартизации...: http://trialektika.narod.ru/conference.htmlhttp://trinitas.ru/rus/doc/0016/001c/00161422.htm Хочу обратить внимание читателей так же на следующие пояснения Проекта. «Тетрасоциология – термин, введенный Львом Семашко в 1999 году для обозначения развиваемого им с 1976 года нового направления теоретической социологии, которая первоначально называлась «Сферный подход». Тетрасоциология (т.е. четырехмерная социология) раскрывает на качественном уровне фрактальную природу общества и возможность его гармонии. Фрактальная иерархическая структура общества раскрывается через взаимовключение и самоподобие матриц сферных показателей ресурсов, процессов, структур и сферных классов населения. Матрицы сферных показателей являются социальными фракталами тетрасоциологии. При наложении на них пропорций «золотого сечения» из математики гармонии Алексея Стахова или других видов математики гармонии получаются социальные фракталы гармонии или фракталы социальной гармонии. Использование пропорций «золотого сечения» в тетрасоциологии позволило Алексею Стахову ввести термин «золотая тетрасоциология», с которым мы вполне согласны, так как он отражает более высокий уровень развития этой теоретической социологии. Примечание. Алексей Стахов выразил в одном из писем ко мне две очень важные мысли: 1. нельзя преувеличивать значение и возможности его математики гармонии, 2. возможны иные варианты математики гармонии, кроме той, которую создал он». Об индексе гармонии «золотой тетрасоциологии» «В данном проекте делается первая (выделено – П.Сергиенко) попытка интеграции математической теории фракталов, математики гармонии и социальных фракталов тетрасоциологии». «Индекс сферной гармонии «золотой тетрасоциологии» представляет собой некоторое число: например, ноль или единица, вокруг которого определяются области (границы) колебания индекса гармонии (в том числе области «+» и « - »)и степень его приближения к максимальному «идеальному» значению, к которому он всегда стремится, но никогда не достигает его». «Индекс сферной гармонии (или гармоничного развития, или сферной гармонизации) будет способен выражать степень гармонизации любой отрасли, региона и страны, а также меру их отклонения и каждой из их сфер, от идеального значения индекса на любой момент их эволюции. В самом общем виде, этот индекс должен выражать значение не только сферных матриц в целом, но и значение любого сферного показателя в любой сферной матрице, а также положительное или минусовое его отклонение (в абсолютных или относительных величинах) от «идеала» или «нормы». «На основе базовой матрицы 4х4 строится бесконечная иерархическая система сферных матриц размерностью: 4х16, 4х64, 4х256 и т.д. Эта система составляет первый, ресурсный, социальный фрактал тетрасоциологии». Очевидно, по описанию и по ссылкам на научную литературу, что данный Проект математической гармонизации фракталов сферной тетрасоциологии составлен только на основании «теории обобщенных гармонических («золотых») пропорций», которая создана А.П.Стаховым. Если бы авторы Проекта были знакомы с другой теорией, то содержание Проекта было бы несколько иным, особенно в трактовке «индекса сферной гармонии «золотой тетрасоциологии».Однако, будем исходить из поставленной задачи в Проекте и разъяснений Л.Семашко в открытой переписке с 6 математиками: «Я вижу задачу математиков проще: ЗАДАНАсистема ЧИСЛОВЫХ сферных матриц с определенным алгоритмом, делающем их фракталами; ТРЕБУЕТСЯ: найти математический аппарат, описывающий (выражающий) гармоничные пропорции (зависимости) ЧИСЕЛ сферных матриц при условии изменения одного или нескольких ЧИСЕЛ этих матриц. Все, как в треугольнике Паскаля, как в Ряду Фибоначчи и т.п.: ТОЛЬКО ЧИСЛА И АЛГОРИТМ и БОЛЬШЕ НИЧЕГО. Природа этих чисел, их происхождение МАТЕМАТИКОВ НЕ ДОЛЖНА ИНТЕРЕСОВАТЬ, я думаю». В теории П.Сергиенко не все, «как в треугольнике Паскаля, как в ряду Фибоначчи». Почему? Потому, что числовой треугольник Паскаля, по своей сущности, не является геометрическим треугольником, как реальным замкнутым пространством, которое имеет реальные форму, меру и границы своей формы бытия. В теории П.Сергиенко первичным математическим объектом является геометрический треугольник, который изначально – пространственная реальность, а потом уже – числовая реальность. Реальное пространство можно рассматривать конкретно, как некую сферу (фракталы сферы) бытия, измерять конкретными единицами мер, производить математические расчеты, имеющие конкретный, а не абстрактный смысл. Очевидно, что, демонстрируемые выше, рисунки Л.Семашко являют собой сферные геометрические матрицы идеальных (квадратных и круговых) фрактальных пространств, отношения которых, в согласии с Проектом, требуется выразить в реальных гармоничных пространственных и числовых мерах. I. Исходя из того, что на базовой матрице 4х4 строится бесконечная иерархическая система сферных матриц размерностью: 4х16, 4х64, 4х256 и т.д., сформулируем поставленную задачу на математическом языке применительно к образно-геометрическим рисункам Л.М.Семашко. То есть нам необходимо выполнить следующее: - Задаться некоторым числом реальной или произвольной меры диаметра круговой сферы в линейных единицах измерения.
- Руководствуясь напутствием Пифагора (Узрите треугольник, и проблема на две трети решена… Все вещи состоят из трех), построить «гармоничный» треугольник, равновеликий четверти данного круга, поскольку изначальная сфера Л.Семашко делится на 4 равновеликие и фрактальные сферы.
- Сложить из 4 фрактальных и равновеликих треугольников фигуру квадрата (прямоугольника) равновеликую данному кругу (сфере).
Таким образом, оговоренные условия возвращают нас как бы к решению древнейшей задачи, так называемой «Задачи квадратуры круга», но к решению ее не просто мерой диаметра круга, а мерой диаметра круга, выраженной в числах его «золотого сечения».
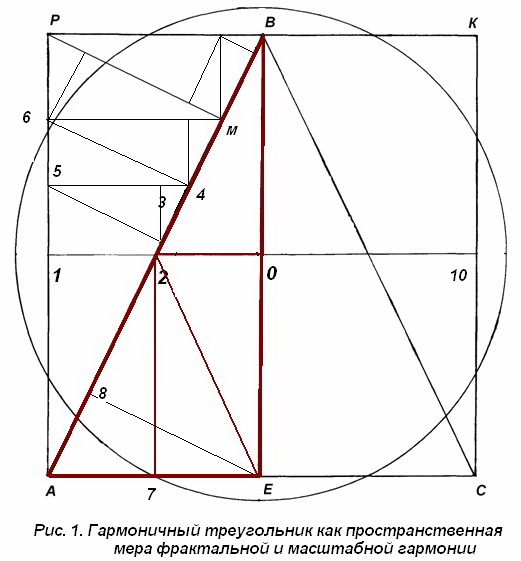
Таким образом, основополагающим условием в решении задачи, обуславливаемой Проектом, является построение базового «гармоничного» треугольника (на Рис.1 выделен красным цветом), равновеликого четверти круга. Пространство базового треугольника должно геометрически бесконечно делиться на фрактальные себе треугольники 4х4, 4х16, 4х64, 4х256 и т.д. Заметим, в истории развития математики гармонии, построение такого треугольника фактически является четвертым фундаментальным открытием после открытий: закона «золотой пропорции» в отношениях между целым и его частями (большая часть так относится к меньшей части, как целое относится к большей части); теоремы Пифагора;открытия чисел «золотого сечения» отрезка(0,6180339…, 1,6180339… и 0,3819661…). Полагаю, что ниже иллюстрируемое решение задачи, инициируемой настоящим Проектом, может внести существенный вклад в становление и развитие МАТЕМАТИКИ ГАРМОНИИ, в том числе – в математизацию развития гармоничной тетрасоциологии. Для решения задачи, изложенной в Проекте, зададимся изначальной,естественной мерой масштабной гармонии. Это может быть мера диаметра молекулы воды, …диаметра Планеты и т.п., которая может быть выражена числовой мерой в метрах, дюймах или др. единицах, или просто произвольным числом. Например, в качестве меры возьмем целое число 2761938. Предположим, что данное число есть мера квадрата гипотенузы прямоугольного треугольника. По данному числу в условном масштабе я вычисляю и строю (Рис.1): 1) гармоничный прямоугольный треугольник АВЕ (алгоритм построения – ноу-хау) 2) из четырех равновеликих прямоугольных треугольников треугольнику АВЕ строю прямоугольник АРКС; 3) по построенному прямоугольнику АРКС, строю равновеликий ему круг. Еще раз заметим, что алгоритм вычислений и построения сторон гармоничного треугольника ниже не описываются, а указываются только полученные результаты вычислений, достоверность которых может проверить любой читатель, знающий теорему Пифагора: Гипотенуза АВ = =1661,9079…; катеты АЕ = ЕС =726,28041…; АР = ВЕ = КС = 1494,8092..., площадь треугольника – 542825,3 кв.ед. 1. Проверим, действительно ли треугольник АВЕ подтверждает имя «гармоничный». Для этого вычислимотношения сторонпрямоугольного треугольника АВЕ, в согласии с законом «золотой» пропорции (Большая часть так относится к меньшей части, как целое к большей части). То есть, больший катет треугольника АВЕ так относится к меньшему его катету, как гипотенуза – к большему катету:

Таким образом,все количественные отношения между сторонами базового гармоничного треугольника состоят из«золотых» чисел. 2. На Рис.1 очевидно и подтверждается вычислениями, что базовый треугольник АВЕ (красный) делится на 4 равновеликих, прямоугольных треугольника: ∆В02 = ∆Е02 = ∆Е72 = ∆А72. Рассмотрим отношение сторон, например, ∆В02, где гипотенуза В2 ≈ 830,954; катет В0 ≈ 747,4046; катет 02 ≈ 363,14023; площадь ∆В02 = 135706,33 кв.ед. 
3. Из 4 базовых равновеликих, фрактальных и гармоничных треугольников строится прямоугольник АРКС, площадь которого равна: 2АЕ х ВЕ = 2 х 726,28041 х 1494,8092 ≈ 2171301,2. Далее строим круг (сферу) равновеликий построенному прямоугольнику АРКС. Радиус круга: r = АВ : 2 ≈ 1661,9079 : 2 ≈ 830,954; Поскольку площадь круга равнаπr2, а r2 = (830,954)2 ≈ 690484,46, то, разделив площадь прямоугольника на значение r2,мы получаем значение числа «пи», как доказательство того, что площадь базового гармоничного треугольника действительно равна одной четвертой части площади круга: π = 2171301,2 : 690484,46 ≈ 3,1446054. Из этого следует, что площадь каждого гармоничного треугольника равна четверти круга, то есть:
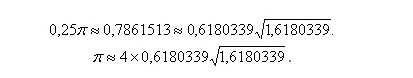
Таким образом, построенный базовый гармоничный ∆АВЕ делится изначально на 4 равновеликих, фрактальных и гармоничных треугольника. Далее, каждый из 4-х гармоничных треугольников в свою очередь может аналогичным образом делиться вновь на 4 фрактальные, гармоничные треугольники и т.д. в последовательных количествах 4, 16, 64, 256, …, формируя непрерывный континуум из фрактальных, гармоничных, треугольных пространств разного масштаба. II. Предположим, что мы не делим некий базовый, гармоничный прямоугольный ∆АВЕ, у которого гипотенуза равна 1, на фрактальные треугольники, а наоборот, складываем из базовых равновеликих и фрактальных треугольников синтетический и фрактальный им треугольник, гипотенуза которого должна быть равна 256. Соответственно, катеты синтетического треугольника, собранного по определенному алгоритму будут равны: 111,8761; 230,26013. Площадь треугольника равна 12880,302 кв.ед. Площадь прямоугольника, собранного из 4 равновеликих треугольников равна: 2х111,8761х230,26013 = 4х12880,302 = 51521,209 кв.ед. Вычисляем отношения сторон синтетического треугольника:

Разумеется, все вычисленные результаты удобно записывать в символьной форме. Если число 1,6180339… обозначить символом Ф, число 0,6180339… – символом ф, число 0,3819661… - символом φ и т.п., то в отношениях данных чисел можно выявить большое количество комбинаторных закономерностей: 1/ф = Ф; 1/Ф = ф; фФ =1; ф2 = φ; … которые обобщенны в работах А.П.Стахова и др. ученых. Например, число «пи» (площади круга) в мерах «золотого сечения» можно записать символами:
В конечном итоге, как следствие выше доказанного, мы можем дать определение гармоничного «треугольника». Гармоничный треугольник – такой треугольник, который может делиться и умножаться бесконечно на фрактальные себе треугольники, отношения (деления и умножения) сторон и площадей которых между собой можно записать числами «золотого сечения» 0,6180339…; 1,6180339… и целыми числами. Резюме. В результате, выше описанных математических операций, можно полагать, что первая попытка интеграции математической теории фракталов и математики гармонии Сергиенко П.Я. в гармоническую фрактальную тетрасоциологию, в согласии с указанным выше Проектом, выполнена. Вместе с тем, автором выявлено, что базовый «гармоничный треугольник», как пространственный объект, может делиться не на один, а на три разных вида «гармоничных» треугольников. Выявленное фундаментальное свойство гармоничного треугольника в свою очередь может стать предпосылкой для исследования и более глубокого развития теории и практики гармоничной тетрасоциологии. Это тема уже другой публикации. Вот так гармонично «переплетается» решение нескольких фундаментальных задач математики и наших представлений о всеобщей гармонии действительности. Полагаю, в этом и есть суть элементарных начал математики гармонии, могущей моделировать формирование бесконечного многообразия пространств жизненных систем. Числовые константы и пространственные формы гармонии, как и форма генетического кода человека, лошади, обезьяны, ... почти изоморфны (фрактальны), но только "почти". Тонкости их отличия – этодругой раздел будущей математики гармонии. Обозначенная автором тропа к познанию выше изложенного, и к другим открытиям – это увлекательная книга (рукопись). Имя ей «Учебно-методическое пособие по элементарной математике гармонии». В ней содержатся не только уже известные знания, но так же совершенно новые знания.Рукопись заслуживает того, чтобы издать ее содержательной, красочной и творчески увлекательной для школьников, студентов и их учителей. Дело за тем, кто может себе это позволить. Автор уверен, вложенные средства окупятся во много крат, а полученные знания – неоценимы. Copyright © Сергиенко П.Я. 7 февраля 2009 Последняя редакция
----------------------------------------------------------------
Дорогой Петр Якубович!
Я восхищаюсь Вашим отношением к задаче и Вашими достижениями. Сейчас я очень занят, через неделю две напишу детальное письмо. Сейчас готовлю рассылки - жду Ваших откликов на них.
С уважением,
Лев Семашко
================================================================================
О началах всеобщего гармоничного образования
Цивилизация в настоящее время, выражаясь сакральным языком, в своем развитии находится на стыке эпох – эпохи «разбрасывания камней» и эпохи «собирания камней». Данная статья является неким предисловием к последующим моим публикациям: «От фрактальной математики гармонии триалектики к фрактальной математике гармонии тетрасоциологии», «Гармоничный треугольник как мера фрактальной гармонии ВСЕГО», «Золотое сечение, задача квадратуры круга и константа тонкой структуры». Очевидно, что эпоха длительного господства мировоззрения диалектического материализма исчерпала свои философские и научные потенции буквально во всех областях познания и практического действия человечества Планеты. Кризис философской онтологии и естествознания, как фундамента мировоззрения, трансформировался в глобальный экологический, финансово-экономический и социальный кризис. Центральным объектом глобального кризиса стал Человек и его мировоззрение, которое есть синтез веры, знаний, убеждений и социально-производственных отношений в триединой ноосферной системе Природа-Человек-Общество. Человек – часть Природы (Творца) и ее творение, часть, наделенная изначально разумом и свободой воли творения вторичной природы своего бытия (Ноосферы). Ни одно другое живое существо на Земле такой свободой воли не обладает, в том числе не обладает даже Творец. Не случайно, данная свобода Человеку в Священном писании оговаривается важными Заповедями его деяний (заостряю внимание на двух из них): · Познай своего Творца, что тождественно – познанию Его законов изначально сотворенного гармоничного бытия Космоса. · Как вы мерите, так и вам будет отмерено, что тождественно познанию пространственных мер и количественных отношений предустановленной гармонии бытия и творения. Можно предположить, что данные заповеди определяют высший смысл предназначения человечества (долгоживущего Человека по Паскалю), как пространственного, интеллектуального и духовного продолжения нашего Творца. Генератором для проявления данной Человеку свободы воли является его мировоззрение, которое косвенно начинает формироваться уже в утробе матери. Дальнейшие основные источники и составные части формирования мировоззрения всем известны. Также известно, что общественным бытием и бытием отдельного человека управляют духовные идеи, среди которых дух веры и дух знания являются определяющими. Они составляют базис духовного мировоззрения. В чем Сущность единства духа веры и духа знания? Дух веры вселяет в нас надежду на будущую хорошую жизнь и позволяет нам выживать. Дух знания вселяет в нас уверенность и любовь к жизни и позволяет нам хорошо жить. Рождение нового знания часто оплодотворяется бессознательной, интуитивной верой, а любое новое знание, подтверждающее интуицию, делает веру осознанной. Взаимопроникновение духа веры и духа знания порождает МУДРОСТЬ. В эпоху господства диалектико-материалистического мировоззрения основная масса людей верила в Творца, в приход справедливого коммунистического будущего, в мощь НТП, в безграничные его возможности по преобразованию Природы и подчинению ее своим материальным интересам. Вера и знание всегда рассматривались как диалектические противоположности. В эпоху идейных, научных, финансово-экономических, экологических кризисов происходит критическое переосмысление и возрождение как бы давно забытого старого на основе новых знаний, в том числе переосмысления фундамента самих ЗНАНИЙ о действительности. Среди появившегося множества мировоззренческих концепций широкое признание и развитие в мире философии, науки и культуры в настоящее время получили триалектика П.Я.Сергиенко и тетрасоциология Л.М.Семашко. Триалектика, как наука о началах гармоничного бытия Природы, а тетрасоциология, как наука о законах гармонии общественного бытия. Известно, что в любой науке столько науки, сколько в ней математики. Математика является неотъемлемой частью научного мировоззрения. Почти в одно и то же время с развитием философских систем триалектики и тетрасоциологии в обществе начали возрождаться и развиваться древние знания математики гармонии. По утверждению одного из ее теоретиков А.П.Стахова http://trinitas.ru/rus/doc/0232/004a/02321088.htm :«… в современной науке создано новое математическое направление, получившее название «Математика Гармонии» [3, 5] и что это направление в своих истоках восходит к одному и тому источнику – «Началам» Евклида, что и «Классическая Математика» (аксиомы Евклида)». Данному математическому направлению исключительно высокую оценку дал автор тетрасоциологии Л.М.Семашко в статье http://trinitas.ru/rus/doc/0232/004a/02321088.htm:«Участие такого выдающегося ученого как профессор Стахов в нашей Международной Академии Гармонии, в которой кафедра Математики Гармонии будет создана одной из первой, значительно повышает научную и экономическую ценность этой Академии и ее привлекательность для мирового сообщества. Академия гармонии и математика гармонии взаимно дополняют, усиливают и обогащают друг друга. Они содействуют взаимному признанию и развитию». Создание математики гармонии – необходимость нашего времени. Об этом говорилось в октябре 2008 года на XVIII Всемирном Конгрессе Международной Ассоциации Педагогов за Мир (МАПМ), объединяющей более 60 тысяч педагогов из почти 100 стран мира. Глобальный Союз Гармонии http://peacefromharmony.org/?cat=home и его Президент Л.М.Семашко исключительно заинтересованы в создании теории и учебников математики гармонии, как фундаментальной научной части гармоничного мировоззрения цивилизации. Вначале члены Правления ГСГ (представители более 15 стран Планеты) ориентировались только на одну математическую теорию гармонии, истоками которой являются НАЧАЛА Евклида и числа Фибоначчи. Однако, когда уже был составлен Проект всеобщего гармоничного образования http://peacefromharmony.org/?cat=ru_c&key=372 и математический к нему проект http://peacefromharmony.org/?cat=ru_c&key=370 в число разработчиков теории математики гармонии был включен автор триалектики П.Я.Сергиенко. Триалектика в последней четверти ХХ века зародилась и развивается изначально как триединство веры, философской онтологии и математического знания о началах гармонии. Это вытекает из цитируемого ее определения: ТРИАЛЕКТИКА – наука о началах гармоничного бытия и творения жизни в согласии с Символом Святой Троицы, Ее принципами бытия и их математическим обоснованием. Мировоззренческим основанием триалектики является синтетическое начало веры в Святую Троицу Бога христиан и веры восточных суфиев в то, что бренный мир в той мере, в какой он реален, не может быть ничем другим, кроме как Богом. Он один в Бытие, и в Надбытие, а весь мир в целом, и какая-либо часть этого мира (духовная или материальная) есть часть божественной реальности. Бога следует искать в своём сердце, а не в Иерусалиме, или Мекке. Истоки математического понимания и объяснения законов гармонии мира теряются в далекой древности. Установлено, например, что знания о равенстве квадрата гипотенузы сумме квадратов катетов были известны за 20 веков до Пифагора, а знание «золотой пропорции» насчитывает более 3 тыс. лет. Применение мер «золотого сечения» выявлено в строениях больших пирамид Гизы и обнаружено на фресках древнеегипетских гробниц. То есть начала математики гармонии были заложены задолго до сформулированных аксиом Евклида, которые являются НАЧАЛАМИ классической математики. Существует множество исторических утверждений знаменитых философов, историков, математиков о том, что теоретические и практические (построения) НАЧАЛ геометрической гармонии космоса были заложены в основном Платоном. Однако его идеи последующие математики либо недостаточно глубоко поняли, либо исказили по причине развития математики в практических целях. В итоге геометрическое деление отрезка равного 1 на гармоничные части 0,6180339… и 0,3819661, осуществленное Евклидом, противоречиво (не корректно) по отношению к его алгебраическому делению, дающему результат 1,6180339… и -0,6180339… Хотя в первом и во втором случае сумма слагаемых частей формально равна 1. Более подробно об этом в документе http://trinitas.ru/rus/doc/0232/010a/02320001.htm В поиске разрешения обнаруженного противоречия триалектическим методом, автором был открыт иной алгоритм геометрического, непротиворечивого деления отрезка прямой на три гармоничные части 1: 1,6180339…, 0,6180339…, 0,3819661…, которые все были со знаком «+». Это открытие в свою очередь привело автора к открытию «гармоничного треугольника», как изначальной меры гармонии Всего, как для одномерного, так и для двумерного пространства – и к другим важным открытиям. 1Сергиенко П.Я. Начала. Триалектика сакральной геометрии. Пущино-2005 Сергиенко П.Я., О началах всеобщего гармоничного образования // «Академия Тринитаризма», М., Эл № 77-6567, публ.15095, 14.02.2009 ------------------------------------------------------------ О началах гармоничной формализации фрактальных матриц тетрасоциологии Геометрия есть познание ВСЕГО сущего (Платон), а ВСЕ есть ЧИСЛО (Пифагор) Логические начала формализации гармоничных отношений
В течении тысячелетий математика формально познает онтологию гармонии ЦЕЛОСТНОСТИ. На протяжении всей истории познания существуют параллельно два формальных метода познания гармонии целого и его частей: диалектический и триалектический.
До третьего тысячелетия преимущественно развивался и господствовал метод формальной диалектики, метод "исключенного третьего".
Формально (по Аристотелю) диалектика гармонии частей и целого выражается как А + В = 1, где 1 – символцелого, а А = В – абсолютноетождество и симметрия двух частей целого. То есть А : В = В : А = 1, что равнозначно А : А = В : В, в результате которого "третьего не дано" (не получено).
Триалектика – методи научная теория познания единства пространственной и количественной гармонии симметрии и асимметрии целого и его частей. Триалектика, исходя из аксиомы, В мире нет такого целого, которое не является частью другого целого, любую часть иерархического устройства пространства мира формально рассматривает как «часть» и, в том же смысле, как «целое». В триалектическом познании развивающееся целое формально состоит из двух неравных частей. Формальной логикой оно выражается как А + В = 1 +1, где А ≠ В – абсолютная, реальнаяа симметрия частей целого, а 1 + 1 = 2 – абсолютная, условная симметрия противоположных частей целого.
Отношения частей А : В = В : А = С; В : А = А : В = D порождают («дают», по Аристотелю), таким образом, новые C и D («третье» и «четвертое»), не нарушая при этом формально-условной симметрии целого. В итоге, гармоничная триалектика целостности формально становится гармоничной "тетралектикой целостной системы отношений ABCD", а в применении к обществу – она может проявляться как "тетраcоциология целостной системы ЛИОВ, по Л.М.Семашко».
С = 1,6180339... и D = 0,6180339.... являются количественными, постоянными мерами отношений в метрике АВСД (ЛИОВ, по Л.М.Семашко). В свою очередь сфера фрактальных отношений A,B,C,D так же порождает внутри себя гармоничные отношения фрактальных пространств, где C и D так же являются константами отношений уже производных от А,В,С,Д. Такова суть изначальной математической формализации тетралектики.
Таким образом, в согласии с Математикой фрактальной ГАРМОНИИ (МФГ) триалектики, формальные тетраотношения принципиально НЕ ограничены пропорциями двух или трех чисел и НЕ бессильны перед пропорциями четырех и более чисел. То есть они вполне формально применимы к целочисленным матрицам Л.Семашко: 4 х 4 = 16; 4 х 16 = 64; 4 х 64 = 256;… Принцип гармоничной формализации целых чисел Любое число формально, и достаточно точно, можно разложить на сумму симметричных и асимметричных гармоничных чисел (его частей), например, с точностью до 8 знака. Аналогично так же его можно умножить, получив ряд новых гармоничных чисел. Руководствуясь логическими началами триалектической формализации, рассмотрим это на конкретных примерах для целых чисел: 1; 2; 3; 4; … десятичного ряда: …+0,0729492+0,1180339+0,1909831+0,3090169+0,5+0,5+0,8090169+1,3090169+2,1180339+3,4270508+ … …+0,1458982+0,2360678+0,3819661+0,6180339 + 1 + 1 + 1,6180339+2,6180339+4,2360678+6,8541017+ … …+0,2188230+0,3541180+0,5729410+0,9270590+1,5+1,5+2,4270590+3,9270590+6,3541180+10,281177+ … …0,29179630+0,4721358+0,7639321+1,2360679 + 2 + 2 + 3,2360679+5,2360679+8,4721358+13,708203+ … ………………………………………………………………………………………………………………
Внимательный читатель должен заметить в данных рядах следующие закономерности:
- Каждый ряд чисел является рекуррентным рядом, которому присущи все без исключения, выявленные на сегодня, комбинаторные закономерности для рекуррентных рядов (так называемых «чисел Фибоначчи»).
- Каждое из средних чисел (красные) каждого ряда являют собой «вещественное» число равное 0,5(А+В). То есть оно являет собой онтологическую меру (половину чего-либо единичного целого). Формально вещественное число является единой мерой в арифметической и геометрической прогрессиях. Арифметическая прогрессия вещественного числа являет собой рекуррентный ряд чисел, которыйобладает определенными пространственными, числовыми и комбинаторными закономерностями. Образованные числами (0,5)р, р = 0; 1; 2; 3;… рекуррентные ряды могут быть выражены, например, красивой, фрактальной, циклично повторяющейся, нумерологической матрицей в целых числах:
- Посредством числовых значений А и В (динамичной половины данного числа) и«вещественного числа» (статичной его половины) мы можем выразить в 3-хи более гармоничных числах любое целое число, а также меру их «золотой» пропорции.
«1»: 0,1909831 + 0,3090169 + 0,5 = 1, где отношения: 0,5 : 0,3090169 = 0,3090169 : 0,1909831 = 1,6180339, являют собой «золотую пропорцию» (ЗП), где отношения: 0,5 х 0,1909831 = (0,3090169)2 = 0,0954915. Аналогичные результаты мы получим для чисел 2; 3; 4; … 10; 16; 64; 256; …
«2»:
0,3819661 + 0,6180339 + 1 = 2. Отношения ЗП: 1 : 0,6180339 = 0,6180339 : 0,3819661 = 1,6180339. Отношения ЗП: 1 х 0,3819661 = (0,6180339)2 = 0,3819661.
«3»:
0,572941 +0,927059 + 1,5 = 3. Отношения ЗП: 1,5 : 0,927059 = 0,927059 : 0,572941 = 1,6180339. Отношения ЗП: 1,5 х 0,572941 = (0,927059)2 = 0,8594383.
Аналогичные результаты отношений мы получим для чисел 4; … 10; 16; 64; 256; … То есть в данных отношениях, деления крайних и средних членов, мы всегда получаем два ряда постоянных числовых значений: 1,6180339… и 0,6180339… При отношениях умножения мы получаем один ряд переменных числовых значений: … 0,0954915; 0,3819661; 0,8594383; …., закономерности которого я не исследовал.
В триалектическом познании отрезок прямой (его часть), круг и другие пространственные объекты, с помощью круговых движений и прямыми линиями (единой мерой кругового движения) «рассекаются» на части в «золотых» отношениях между собой и целым,не на две части, а – на три. То есть, каждое конкретное число содержит в себе как бы эквивалент пространственной меры в «золотом» отношении. Все выше сказанное позволяет нам утверждать, что любое целое число можно выразить суммой 2-х и более иррациональных и рациональных чисел, находящихся между собой в отношениях 0,6180339… и 1,6180339…То есть каждое число тетрасоциологических целочисленных матриц Л.М.Семашко можно расчленить на бесконечное множество (2 +р) гармоничных частей, где р = 0, 1, 2, 3, … , чтопродемонстрировано матрицей из рекуррентных рядов «вещественных» чисел меньше 1. А в роли вещественного числа, что доказано выше, может выступать любое число, как изначально задаваемое число рекуррентного ряда. Нумерологическая матрица рекуррентных рядов «вещественных» чисел, где первая строка начинается с вещественного числа (0,5)0 = (4)0 = (16)0 = (64)0 =…= 1.
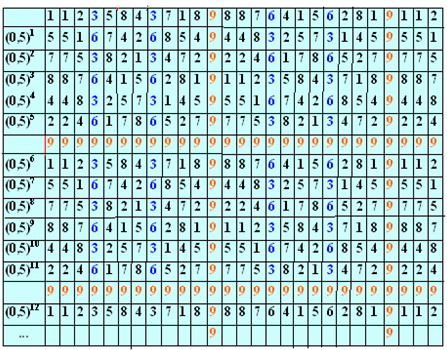
В данной матрице как бы зашифрованы в целых числах их изначальные, вещественные, количественные меры гармоничных отношений структур (нумерологических ячеек) некой целостной системы.
Copyright © Сергиенко П.Я.
12/11/08
Сергиенко П.Я. НАЧАЛА МАТЕМАТИЗАЦИИ ГАРМОНИИ. ЗАДАЧА (ПРЕДЛОЖЕНИЕ II.11) ЕВКЛИДА И АЛГОРИТМ ЕЕ РЕШЕНИЯ Выставить на обозрение свой алгоритм решения озаглавленной задачименя позвали публикации: С.А.Ясинского http://trinitas.ru/rus/doc/0232/009a/02321170.htm и А.П.Стахова,И.Г.Райлян, (http://trinitas.ru/rus/doc/0232/100a/02320015.htm). Из данных публикаций я выяснил, как и предполагал ранее, что «Предложение 2.11» Евклида,так же как известная «Задача квадратуры круга»,пришли в обобщенные знания НАЧАЛ с более древних эпох цивилизации. Алгоритмы его решения в течение тысячелетий предлагались разные. Онтологические изъяны энциклопедического алгоритма «золотого сечения» катета прямоугольного треугольника (как отрезка) я уже частично критиковал и предложил свой алгоритм. Читателям сайта он давно известен и критических замечаний на него не последовало. В последние годы я занимаюсь исследованием явления гармонии (мер и пропорций) в двухмерном пространстве. Выявлены такие геометрические фигуры, как «гармоничные прямоугольные треугольники», их меры, свойства и закономерности в самоорганизации пространства. В этой связи получил замечание-предложение от профессора С.Л.Василенко по поводу отсутствия в предложенном мной методе математизации гармонии плавного перехода от одномерного пространства к двумерному. Почему я этого не сделал раньше? Возможно, этому мешало отсутствие у меня знания об истинном содержании изначальной формулировки задачи («Предложения 2.11) в НАЧАЛАХ Евклида. Я пользовался формулировками, которые в разных вариациях часто приводил в своих статьях А.П.Стахов. Например, в публикации http://trinitas.ru/rus/doc/0232/004a/02321051.htmонпишет: «В Книге II своих «Начал» Евклид сформулировал предложение 2.11, которое задает «деление отрезка в среднем и крайнем отношении»: Предложение 2.11. Данную прямую разделить так, чтобы прямоугольник, заключенный между целой и одним из отрезков, был равен квадрату на оставшемся отрезке. Рассмотрим это определение более детально. Для этого возьмем отрезок АВ и разделим его точкой С на две неравные части АС и СВ (Рис.1)…». И вот большая удача! В упомянутых статьях приводится без искажений понятная формулировка из «НАЧАЛ» Евклида (ПРЕДЛОЖЕНИЕ 2.11): «Данную прямую АD разделить на две неравные части АF и FD так, чтобы площадь квадрата, построенного на большем отрезке AF, равнялась бы площади прямоугольника, построенного на отрезке АD и меньшем отрезке FD». К истории и содержанию данной задачи в вышеназванных и других публикациях имеются пространные комментарии (Мордухай-Болтовского, Ясинского, Стахова, Белянина...), в которых проявляются разночтения. Абстрагируемся от них. Существует мнение, что в правильном и четком логическом смысле сформулированной задачи содержится 50%ее решения. В этой связи хочу заметить, что в формулировке данной задачи есть математическая некорректность. Возможно, это описка или ошибка перевода. Трудно поверить, что Евклид не понимал различия между отрезком и прямой, поскольку прямая не имеет границ. А и D – точки границ, обозначающие некую часть прямой, которую предложено самим Евклидом называть отрезком прямой. Начало формулировки задачи в древнем греческом оригинале вероятнее всего начинается так: «Данный отрезок АD прямой разделить…». Однако, перейдем к смыслу предложенной задачи. Поскольку в задаче речь идет о построении равновеликих прямоугольников и квадрата на основании произвольного отрезка прямой, то логично признать, что данная задача – это задача из серии классических геометрических построений пространственных мер, с помощью циркуля и линейки. Напомним, что в данной классике геометрических построений на плоскости, линейка без делений служит только для проведения прямых линий и соединения прямой линией точек на плоскости. Циркуль служит для черчения окружностей, установления изначальной произвольной меры отрезка прямой, деления отрезка посредством круговой проекции на равные и не равные части, восстановления перпендикуляра к прямой в заданной точке, наложения меры длины одного отрезка намеру длины другого и их вычитания, переноса меры отрезка круговой проекцией из одной геометрической фигуры на другую, а так же для суммирования длин отрезков. А теперь приступим к решению сформулированной Евклидом задачи. ПРИМЕЧАНИЕ.Вместо буквенного обозначения геометрических объектов автор пользуется цифровым, что значительно повышает быстроту ориентации в рисунках с большим количеством обозначенных точек.При этом обозначается, например, 1-12 (отрезок),A,4,8,D (периметр и площадь геометрической фигуры).
Алгоритмы решения задачи. А). Алгоритм геометрического построения (Рис.1): 1.На прямой строим отрезок АD, для чего произвольным раствором циркуля с центром в точке 0 чертим полуокружность, пересекающую линию в точках А и D. При данном построении А-0 = 0-D – радиус окружности, меру которого мы принимаем равной 1. Отрезок АD = 2. 2.К точке 0 восстанавливаем перпендикуляр. 3.Отрезок А-0 делим на две равные части, где А-1 = 1-0 = 0,5. 4.Соединяем прямой точку 1 с точкой 2 (пересечения окружности) и перпендикуляра. 5.Раствором циркуля 1-2 на отрезке АD откладываем отрезок А-13 = 1-2. 6.Ставим ножку циркуля в точу 13 и радиусом 13-D отмеряем отрезок FD. 7.К точкам A;F;13;D восстанавливаем перпендикуляры. 8.Раствором циркуля AF откладываем на перпендикулярах точки 3 и 5. 9.Соединяем прямой точки 3 и 5. В итоге, на отрезке АF построен квадрат A,3.5,F. 10.Ставим ножку циркуля в точку D и раствором циркуля FDна перпендикуляре откладываем точку 8. 11.В точке 8 восстанавливаем перпендикуляр до пересечения с А-3 в точке 4. В итоге, на отрезке AD построен прямоугольник A,4,8,D. 12.Ставим ножку циркуля в точку D и раствором циркуля ADна перпендикуляре откладываем точку 7. 13.В точке 7 восстанавливаем перпендикуляр до пересечения в точке 6 с перпендикуляром из точки F. 14.Соединяем прямой точки 6 и 7. В итоге, на отрезке FD, который равен прямоугольнику A,4,8,D построен прямоугольник F,6,7,D. Таким образом, в согласии с Предложением 2.11 на отрезке равном диаметру круга, мерой его радиуса построены квадрат и два равновеликих ему прямоугольника. Пользуясь геометрическим основанием осуществленного построения, я выполнил аналогичное построение на отрезке 0-D = 1 (радиусе круга).
Б). Алгоритм вычисления мер параметров построенных геометрических фигур:
1. В согласии с теоремой Пифагора вычисляем сторону 1-2 прямоугольного ∆1,2,0, где 0-2 = 1, по условию, а 1-0 = 0,5, по построению.1-2 = √1,25 ≈ 1,1180339. 2. Вычисляем построенные отрезки на прямой: 1-13 = 1-2 = 1,1180339 по построению; 0-13 = 1-13 – 1-0 = 1,1180339 – 0,5 ≈ 0,6180339; А-13 = А-0 + 0-13 = 1 + 0,6180339 ≈ 1,6180339; 13-D = 0-D – 0-13 = 1 – 0,6180339 ≈ 0,3819661; FD = 2x13-D = 2x0,3819661 ≈ 0,7639322 по построению; AF = AD – FD = 2 – 0,7639322 ≈ 1,2360678; 0-F = 0-D – FD = 1 – 0,7639322 ≈ 0,2360678; 3. Вычисляем площади построенных квадратов и прямоугольников: Площадь квадрата A,3,5,F – (АF)2 = (1,2360678)2 = 1,5278636; Площади равных прямоугольников F,6,7,Dи A,4,8,D– 2 х 0,7639322 = 1,5278644; Площадь квадрата A,10,7,D– (АD)2 = 22 = 4; Площадь квадрата 0,2,18,D– (0-D)2 = 12 = 1; Площадь квадрата 0,15,116,13– (0-13)2 = (0,6180339)2 = 0,3819661; Площади прямоугольников 0,19,17,Dи 13,12,18,D– 1 х 0,3819661 = 0,3819661. В). Пропорциональные меры отношения длин построенных отрезков на мере длины отрезка AD: AF/FD = 1,2360678/0,7639322 ≈ 1,6180333; AD/AF = 2/1,2360678 ≈ 1,6180342; 0-13/13-D = 0,6180339/05819661 ≈ 1,6180333; 0-D/0-13 = 1/0,6180339 ≈ 1,6180342; F-13/0-F = 0,3819661/0,2360678 ≈ 1,6180355; Г). Пропорциональные меры отношения построенных площадей: SA,10,7,D/SA,3,5,F = 4/1,5278644 ≈ 2,6180333 ≈ (1,6180337)2; S0,2,18,D/S0,15,16,13 = 1/0,3819661 ≈ 2,6180333 ≈ (1,6180337)2. Таким образом, мной выполнено «Предложение 2.11.» НАЧАЛ Евклида в строгом соответствии с его формулировкой. И даже перевыполнено. То есть, для сравнения геометрическое построение осуществлено на масштабной мере длины разных отрезков. В этой связи не могу обойти стороной, логику, а точнее, алогичность решения данной задачив статье А.П. Стахова, И.Г. Райлян, «Золотая» научная парадигма: этапы большого пути от Пифагора, Платона и Евклида до «Математики Гармонии» http://trinitas.ru/rus/doc/0232/004a/02321100.htm Цитирую: «Вникнем в суть этой задачи. Для этого изобразим эту задачу геометрически (Рис. 1)». Далее приводится образный рисунок («Рисунок 1. Деление отрезка в крайнем и среднем отношении»), на котором изображены, как бы уже построенные, по условию задачи, (кем то?) равновеликие квадрат и прямоугольник. Далее следует переход к записи в символах отношения отрезков AF/FD, составление символической пропорции (2) и утверждение, что «Пропорция (2) имеет следующую геометрическую трактовку: разделить заданный отрезок на две неравные части в такой пропорции, что отношение…»в конечном итоге приводит калгебраическому уравнению x2 = x +1. И в итоге следует заключение: «Положительный корень этого уравнения Ф = и есть то знаменитое иррациональное число, которое имеет в современной науке много замечательных названий: золотое число, золотое сечение, золотая пропорция, божественная пропорция». Уважаемые авторы, вы описываете алгоритм решения конкретной задачи, в которой нет даже слов «пропорция» и «отношение», а требуется только построить равновеликие квадрат и прямоугольник на не равных частях данного отрезка. Решение задачи заканчивается пунктомБ). Алгоритм вычисления мер параметров построенных геометрических фигур. Действий, изложенных мной в пунктах В) и Г), задача не требует. Это уже относится к математическому развитию последствий решения Предложения 2.11. Строгое, пунктуальное решение этой задачи выводит нас на истинный путь математического познания и моделирования гармонии действительности. Внимательный читатель уже заметил на Рис.1 ∆A,9,Dи ∆A,14,D. Это гармоничные треугольники. Я вернусь к ним в следующей публикации. Внимательный читатель так же заметил, что отрезок равный 1 автором геометрически разделен не на две, а – на три части в равных отношениях. То есть: 1/0,618… = 0,618/0,381… = 0,381/0,236067… ≈ 1,61803… Такое деление целого на части свидетельствует о том, что возрастающий рекуррентный ряд, аналогичный ряду Фибоначчи, может изначально существовать в виде трансцендентных мер пространственной действительности и их гармоничных отношений: … + …0,23606… + 0,38196… + 0,61803… + 1 + 1,61803… + …, а не начинаться с 7-го порядкового числа ряда Фибоначчи, с которого в отношениях чисел начинают проявляться константы гармонии 1,61803... и 0,61803.… Об упомянутых логических началах формализации гармоничных отношений я уже писал в статье http://trinitas.ru/rus/doc/0232/009a/02321105.htm. 3 ноября 2009. --------------------------------------------------------------
Up
|
